
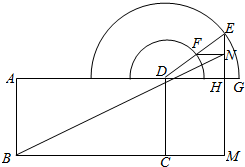
 如图所示,长方形ABCD中,AB=2,BC=4,以D为圆心的两个圆心半圆,半径分别为1和2,G为大半圆直径的右端点,E为大半圆上的一个动点,DE与小半圆交于点F,EM⊥BC,垂足为M,EM与大半圆直径交于点H,FN⊥EM,垂足为N.
如图所示,长方形ABCD中,AB=2,BC=4,以D为圆心的两个圆心半圆,半径分别为1和2,G为大半圆直径的右端点,E为大半圆上的一个动点,DE与小半圆交于点F,EM⊥BC,垂足为M,EM与大半圆直径交于点H,FN⊥EM,垂足为N.分析 (Ⅰ)过F作FQ⊥AG于Q,可得∠GDF=30°,可得MN=MH+QF=2+sin30°,计算可得;
(Ⅱ)设∠GDE=α,α∈[0,π],可得△BMN的面积为S=$\frac{1}{2}$•(sinα+2)•(2cosα+4)=4+2(sinα+cosα)+sinαcosα,令t=sinα+cosα,由二次函数区间的最值可得.
解答 解:(Ⅰ)过F作FQ⊥AG于Q.∵∠GDF=30°,
∴MN=MH+HN=MH+QF=2+sin30°=$\frac{5}{2}$;
(Ⅱ)设∠GDE=α,α∈[0,π],
则MN=MH+HN=sinα+2,BM=BC+CM=2cosα+4,
∴△BMN的面积为S=$\frac{1}{2}$•(sinα+2)•(2cosα+4),
∴S=4+2(sinα+cosα)+sinαcosα,
令t=sinα+cosα=$\sqrt{2}$sin(α+$\frac{π}{4}$),
则t∈[-1,$\sqrt{2}$],且sinαcosα=$\frac{1}{2}$(t2-1),
则S=$\frac{1}{2}$t2+2t+$\frac{7}{2}$=$\frac{1}{2}$(t+2)2+$\frac{3}{2}$,
当t=$\sqrt{2}$,即α=$\frac{π}{4}$时,S取最大值,
故△BMN面积的最大值为$\frac{9+4\sqrt{2}}{2}$
点评 本题考查三角函数恒等变换的实际应用,涉及三角形的面积和二次函数区间的最值,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
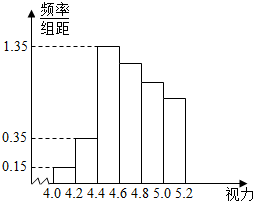 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.| 年级名次 是否近视 | 1~50 | 951~1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
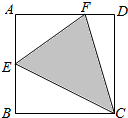 如图,四边形ABCD为正方形,E为AB的中点,F为AD上靠近D的三等分点,若向正方形内随机投掷一个点,则该点落在△CEF内的概率为( )
如图,四边形ABCD为正方形,E为AB的中点,F为AD上靠近D的三等分点,若向正方形内随机投掷一个点,则该点落在△CEF内的概率为( )| A. | $\frac{9}{16}$ | B. | $\frac{7}{16}$ | C. | $\frac{7}{12}$ | D. | $\frac{5}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com