
分析 讨论当|x+1|≥x+2,|x+1|<x+2时,求出f(x)的解析式,由单调性可得最小值.
解答 解:当|x+1|≥x+2,即x+1≥x+2或x+1≤-x-2,
解得x≤-$\frac{3}{2}$时,f(x)=|x+1|,递减,
则f(x)的最小值为f(-$\frac{3}{2}$)=|-$\frac{3}{2}$+1|=$\frac{1}{2}$;
当|x+1|<x+2,可得x>-$\frac{3}{2}$时,f(x)=x+2,递增,
即有f(x)>$\frac{1}{2}$,
综上可得f(x)的最小值为$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查函数的最值的求法,考查绝对值不等式的解法,注意运用分类讨论的思想方法,以及函数的单调性,属于中档题.


科目:高中数学 来源: 题型:选择题
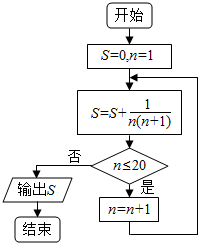
| A. | $\frac{19}{20}$ | B. | $\frac{20}{21}$ | C. | $\frac{21}{22}$ | D. | $\frac{22}{23}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
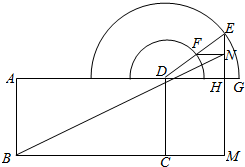 如图所示,长方形ABCD中,AB=2,BC=4,以D为圆心的两个圆心半圆,半径分别为1和2,G为大半圆直径的右端点,E为大半圆上的一个动点,DE与小半圆交于点F,EM⊥BC,垂足为M,EM与大半圆直径交于点H,FN⊥EM,垂足为N.
如图所示,长方形ABCD中,AB=2,BC=4,以D为圆心的两个圆心半圆,半径分别为1和2,G为大半圆直径的右端点,E为大半圆上的一个动点,DE与小半圆交于点F,EM⊥BC,垂足为M,EM与大半圆直径交于点H,FN⊥EM,垂足为N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{x}$=(-x)${\;}^{\frac{1}{2}}$ | B. | x${\;}^{-\frac{1}{5}}$=-$\root{5}{x}$ | C. | (-x)${\;}^{\frac{2}{3}}$=x${\;}^{\frac{2}{3}}$ | D. | x${\;}^{\frac{2}{6}}$=x${\;}^{\frac{1}{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | [-2,1)∪(1,+∞) | C. | (-2,+∞) | D. | (-2,1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
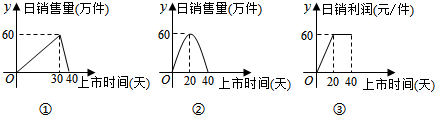
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com