
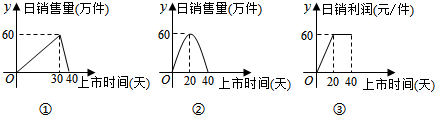
���� ��1������ͼ��д���ֶκ������ɵù����г�����������g��t������λ�������������ʱ��t����λ���죩�Ĺ�ϵʽ��
��2��д����ҹ�˾������������Q��t���Ľ���ʽQ��t��=q��t��•[f��t��+g��t��]���ɣ�
��� �⣺��1�������⣬f��t��=$\left\{\begin{array}{l}{2t��0��t��30}\\{-6t+240��30��t��40}\end{array}\right.$��
g��t��=at��t-40������60=20a��20-40������a=-$\frac{3}{20}$
��g��t��=-$\frac{3}{20}$t2+6t��0��t��40��
��2��q��t��=$\left\{\begin{array}{l}{3t��0��t��20}\\{60��20��t��40}\end{array}\right.$
����ҹ�˾������������Q��t���Ľ���ʽ��
Q��t��=q��t��•[f��t��+g��t��]=$\left\{\begin{array}{l}{-\frac{9}{20}{t}^{3}+24{t}^{2}��0��t��20}\\{-9{t}^{2}+480t��20��t��30}\\{-9{t}^{2}+14400��30��t��40}\end{array}\right.$��
���� ���⿼�麯��ģ�͵�ѡ����Ӧ�ã�����������۵�˼�룬ע����ⷽ���Ļ��ۣ������е��⣮


 ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д� Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д� ������������Ծ�ϵ�д�
������������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{2}$ | B�� | $\frac{1}{2}$ | C�� | -$\frac{\sqrt{3}}{2}$ | D�� | $\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
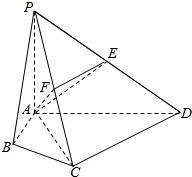 ������P-ABCD�У���ABC=��ACD=90�㣬��BAC=��CAD=60�㣬PA��ƽ��ABCD��EΪPD���е㣬PA=2AB=2��
������P-ABCD�У���ABC=��ACD=90�㣬��BAC=��CAD=60�㣬PA��ƽ��ABCD��EΪPD���е㣬PA=2AB=2�� �鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
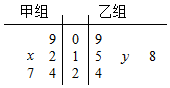 ��ͼ��Ҷͼ��¼�˼ס������������ѧ����һ��Ӣ�����������еijɼ�����λ���֣�����֪�������ݵ�ƽ����Ϊ18���������ݵ���λ��Ϊ16����x��y��ֵ�ֱ�Ϊ��������
��ͼ��Ҷͼ��¼�˼ס������������ѧ����һ��Ӣ�����������еijɼ�����λ���֣�����֪�������ݵ�ƽ����Ϊ18���������ݵ���λ��Ϊ16����x��y��ֵ�ֱ�Ϊ��������| A�� | 18��6 | B�� | 8��16 | C�� | 8��6 | D�� | 18��16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 3��-11 | C�� | -3 | D�� | -3��11 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
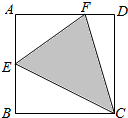 ��ͼ���ı���ABCDΪ�����Σ�EΪAB���е㣬FΪAD�Ͽ���D�����ȷֵ㣬���������������Ͷ��һ���㣬��õ����ڡ�CEF�ڵĸ���Ϊ��������
��ͼ���ı���ABCDΪ�����Σ�EΪAB���е㣬FΪAD�Ͽ���D�����ȷֵ㣬���������������Ͷ��һ���㣬��õ����ڡ�CEF�ڵĸ���Ϊ��������| A�� | $\frac{9}{16}$ | B�� | $\frac{7}{16}$ | C�� | $\frac{7}{12}$ | D�� | $\frac{5}{12}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 5 | C�� | 6 | D�� | $3+2\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com