
分析 (1)由奇函数性质得f(x)+f(-x)=${log}_{2}\frac{1-ax}{1+x}+lo{g}_{2}\frac{1+ax}{1-x}$=0,由此能求出a.
(2)当a=-1时,g(x)=f(x)-log2(mx)=-log2(mx)=0,得x=$\frac{1}{m}$,不存在非零实数m使得函数g(x)恰好有两个零点;当a=1时,g(x)=f(x)-log2(mx)=$lo{g}_{2}\frac{1-x}{(1+x)•mx}$=0,得不存在非零实数m使得函数g(x)恰好有两个零点.
解答 解:(1)∵函数$f(x)={log_2}\frac{1-ax}{1+x}$是奇函数,
∴f(x)+f(-x)=${log}_{2}\frac{1-ax}{1+x}+lo{g}_{2}\frac{1+ax}{1-x}$
=$lo{g}_{2}(\frac{1-ax}{1+x}×\frac{1+ax}{1-x})$=0,
∴$\frac{1-ax}{1+x}×\frac{1+ax}{1-x}$=1,
∴1-a2x2=1-x2,
解得a=1或a=-1(舍)
故a=1.
(2)不存在非零实数m使得函数g(x)恰好有两个零点,理由如下:
a=1,g(x)=f(x)-log2(mx)=$lo{g}_{2}\frac{1-x}{1+x}$-log2(mx)=$lo{g}_{2}\frac{1-x}{(1+x)•mx}$,
由$lo{g}_{2}\frac{1-x}{(1+x)•mx}$=0,得$\frac{1-x}{(1+x)mx}$=1,不存在非零实数m使得函数g(x)恰好有两个零点.
综上,不存在非零实数m使得函数g(x)恰好有两个零点.
点评 本题考查实数值的求法,考查函数是否有两个零点的判断与求法,是中档题,解题时要认真审题,注意奇函数性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | v(t)=-4t+8 | B. | v(t)=4t-8 | C. | v(t)=-8t+2 | D. | v(t)=8t-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
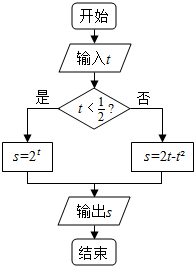
| A. | [0,1] | B. | [$\frac{3}{4}$,$\sqrt{2}$] | C. | [0,$\sqrt{2}$] | D. | [1,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
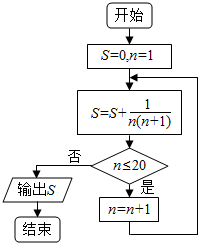
| A. | $\frac{19}{20}$ | B. | $\frac{20}{21}$ | C. | $\frac{21}{22}$ | D. | $\frac{22}{23}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
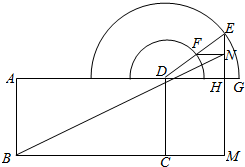 如图所示,长方形ABCD中,AB=2,BC=4,以D为圆心的两个圆心半圆,半径分别为1和2,G为大半圆直径的右端点,E为大半圆上的一个动点,DE与小半圆交于点F,EM⊥BC,垂足为M,EM与大半圆直径交于点H,FN⊥EM,垂足为N.
如图所示,长方形ABCD中,AB=2,BC=4,以D为圆心的两个圆心半圆,半径分别为1和2,G为大半圆直径的右端点,E为大半圆上的一个动点,DE与小半圆交于点F,EM⊥BC,垂足为M,EM与大半圆直径交于点H,FN⊥EM,垂足为N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com