
已知 .求证:
.求证: .
.
证明过程见试题解析.
【解析】
试题分析:本题属于三角恒等式的证明,三角恒等式的证明方法灵活多样,可总结如下:(1)从一边开始直接推证等于另一边,一般地,如果所证等式一边比较复杂而另一边比较简单时多采用此法,即由繁到简;(2)左右归一法,即将所证恒等式左,右两边同时推导变形,直接推得左右两边都等于同一个式子;(2)比较法,即设法证明“左边-右边=0”,或“左边/右边=1”;(4)分析法,从被证的等式出发,逐步地探求使等式成立的充分条件,一直到已知条件或显然成立的结论为止,就可以判断原等式成立.本题适用于第四类,观察发现条件中所给角为 ,结论中所给角为
,结论中所给角为 ,可将所证等式利用倍角公式展开,可化为
,可将所证等式利用倍角公式展开,可化为 又由条件将正切化为正余弦可得
又由条件将正切化为正余弦可得 .等式成立.
.等式成立.
【解析】
因为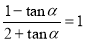 ,所以1+
,所以1+ ,
,
从而, ,
,
另一方面:要证 ,
,
只要证: ,
,
即证  ,
,
即证  ,
,
由 可得
可得 成立,
成立,
于是命题得证.
考点:三角恒等变形.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源:2015届安徽省铜陵市高二下学期月考数学试卷(解析版) 题型:选择题
设F1,F2是椭圆 =1的左、右两个焦点,若椭圆上满足PF1⊥PF2的点P有且只有两个,则离心率e的值为( )
=1的左、右两个焦点,若椭圆上满足PF1⊥PF2的点P有且只有两个,则离心率e的值为( )
A. B.
B. C.
C. D.
D. .
.
查看答案和解析>>
科目:高中数学 来源:2015届安徽师大附中高二下学期期中考查理科数学试卷(解析版) 题型:选择题
若动点 与定点
与定点 和直线
和直线 的距离相等,则动点
的距离相等,则动点 的轨迹是( )
的轨迹是( )
A.椭圆 B.双曲线 C.抛物线 D.直线
查看答案和解析>>
科目:高中数学 来源:2015届安徽师大附中高二下学期期中考查文科数学试卷(解析版) 题型:选择题
如果椭圆 的弦被点(4,2)平分,则这条弦所在的直线方程是 ( )
的弦被点(4,2)平分,则这条弦所在的直线方程是 ( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届宁夏高二下学期期中考试理科数学试卷(解析版) 题型:解答题
已知函数 为常数,e=2.71828…是自然对数的底数),曲线
为常数,e=2.71828…是自然对数的底数),曲线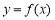 在点
在点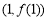 处的切线与x轴平行.
处的切线与x轴平行.
(1)求k的值,并求 的单调区间;
的单调区间;
(2)设 ,其中
,其中 为
为 的导函数.证明:对任意
的导函数.证明:对任意 .
.
查看答案和解析>>
科目:高中数学 来源:2015届宁夏高二下学期期中考试文科数学试卷(解析版) 题型:选择题
对于任意的两个实数对(a, b)和(c, d),规定(a, b)=(c, d)当且仅当a=c ,b=d;运算
“ ”为:
”为: ,运算“
,运算“ ”为:
”为:
 ,设
,设 ,若
,若
则 ( )
( )
A. B.
B.  C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com