

分析 (I)根据直角三角形的射影定义进行求解即可
(Ⅱ)建立空间坐标系,设出F的坐标,利用向量法求出平面的法向量,利用向量法结合二面角的余弦值求出F的位置即可得到结论.
解答  解:(Ⅰ)∵在矩形ABCD中,AB=2,AE=$\frac{1}{4}$AB=$\frac{1}{2}$,D点在平面ABC的正投影恰好能与E重合,
解:(Ⅰ)∵在矩形ABCD中,AB=2,AE=$\frac{1}{4}$AB=$\frac{1}{2}$,D点在平面ABC的正投影恰好能与E重合,
∴DE⊥平面ABC,DE⊥AB,
则在直角三角形ABD中,AD2=AE•AB=$\frac{1}{2}×2$=1,即AD=1
则线段AD的长为1;
(Ⅱ)过B作ABC的直线,
建立以B为坐标原点,BC,BA分别为x,y轴的空间直角坐标系如图:
则BE=$\frac{3}{2}$,DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\frac{\sqrt{3}}{2}$,BC=AD=1
则B(0,0,0),E(0,$\frac{3}{2}$,0),D(0,$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),
C(1,0,0),
设$\overrightarrow{DF}$=λ$\overrightarrow{CD}$=λ(-1,$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),
设F(x,y,z),
则(x,y,z)=(-λ,$\frac{3}{2}$λ,$\frac{\sqrt{3}}{2}$λ)+(-1,$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$)=(-1+λ,$\frac{3}{2}$(λ+1),$\frac{\sqrt{3}}{2}$(λ+1)),
则$\overrightarrow{BE}$=(0,$\frac{3}{2}$,0),$\overrightarrow{BF}$=(-1+λ,$\frac{3}{2}$(λ+1),$\frac{\sqrt{3}}{2}$(λ+1)),$\overrightarrow{BD}$=(0,$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),
设平面EBF的法向量为$\overrightarrow{n}$=(x,y,z),
则$\overrightarrow{n}$•$\overrightarrow{BE}$=$\frac{3}{2}$y=0,$\overrightarrow{n}$•$\overrightarrow{BF}$=(-1+λ)x+$\frac{3}{2}$(λ+1)y+$\frac{\sqrt{3}}{2}$(λ+1)z=0,
即y=0,(-1+λ)x+$\frac{\sqrt{3}}{2}$(λ+1)z=0,
令z=2,则x=$\frac{\sqrt{3}(1+λ)}{1-λ}$,即$\overrightarrow{n}$=($\frac{\sqrt{3}(1+λ)}{1-λ}$,0,2),
设平面BFD的法向量为$\overrightarrow{m}$=(x,y,z),
则$\overrightarrow{m}$•$\overrightarrow{BF}$=(-1+λ)x+$\frac{3}{2}$(λ+1)y+$\frac{\sqrt{3}}{2}$(λ+1)z=0,)),$\overrightarrow{m}$•$\overrightarrow{BD}$=$\frac{3}{2}$y+$\frac{\sqrt{3}}{2}$z=0,
令z=$\sqrt{3}$,则y=-1,x=0,
即$\overrightarrow{m}$=(0,-1,$\sqrt{3}$),
则|cos<$\overrightarrow{m}$,$\overrightarrow{n}$>|=|$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$|=$\frac{2\sqrt{3}}{\sqrt{1+3}•\sqrt{4+\frac{3(1+λ)^{2}}{(1-λ)^{2}}}}$=$\frac{\sqrt{3}}{2}$,
平方得4+$\frac{3(1+λ)^{2}}{(1-λ)^{2}}$=4,得$\frac{3(1+λ)^{2}}{(1-λ)^{2}}$=0,即λ=-1,
即$\overrightarrow{DF}$=-$\overrightarrow{CD}$,即$\overrightarrow{DF}$=$\overrightarrow{DC}$,即F与C重合时,满足条件.
此时$\frac{DF}{CD}$=1.
点评 本题主要考查面面垂直判定以及二面角的求解,建立空间直角坐标系,利用向量法进行求解,综合性较强,运算量较大.


科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∧(¬q) | C. | (¬p)∧q | D. | p∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
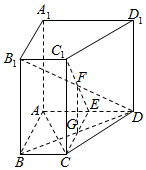 如图,在四棱柱ABCD-A1B1C1D1中,AC⊥B1D,BB1⊥底面ABCD,E为线段AD上的任意一点(不包括A、D两点),平面CEC1与平面BB1D交于FG.
如图,在四棱柱ABCD-A1B1C1D1中,AC⊥B1D,BB1⊥底面ABCD,E为线段AD上的任意一点(不包括A、D两点),平面CEC1与平面BB1D交于FG.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${C}_{n}^{m}$=${C}_{n}^{n-m}$ | B. | ${C}_{m}^{m}$+${C}_{m}^{m-1}$=${C}_{m+1}^{m}$ | ||
| C. | ${C}_{5}^{1}$+${C}_{5}^{2}$=${C}_{5}^{3}$ | D. | ${C}_{n+1}^{m}$=${C}_{n}^{m-1}$+${C}_{n-1}^{m}$+${C}_{n-1}^{m-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 2个 | C. | 3个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com