Question

9．过△ABC所在平面α外一点P作PO⊥α，垂足为O，连接PA，PB，PC．
①若PA=PB=PC，则点O是P的外心；
②若点P到△ABC三边所在直线的距离都相等，则点O是△ABC的内心；
③若PA⊥PB，PB⊥PC，PA⊥PC，则点O是△ABC的垂心；
④若PA，PB，PC与平面α所成的角都相等，则点O是△ABC的外心；
上面选项中正确的序号是①③④．

Answer 1

分析 ①点P为△ABC所在平面外一点，PO⊥平面ABC，垂足为O，若PA=PB=PC，可证得△POA≌△POB≌△POC，从而证得OA=OB=OC，符合这一性质的点O是△ABC外心；
②点P到△ABC的三边距离相等，可得O到三边的距离相等；
③连接AO并延长交BC于一点E，连接PO，由于PA，PB，PC两两垂直可以得到PA⊥面PBC，而BC?面PBC，可得BC⊥PA，由PO⊥平面ABC于O，BC?面ABC，PO⊥BC，可得BC⊥AE，同理可以证明才CH⊥AB，又BH⊥AC．故H是△ABC的垂心；
④），∠PAO=∠PBO=∠PCO⇒AO=BO=CO⇒O为三角形的外心．

解答 解：①点P为△ABC所在平面外一点，PO⊥平面ABC，垂足为O，若PA=PB=PC，
故△POA，△POB，△POC都是直角三角形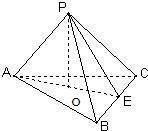
∵PO是公共边，PA=PB=PC
∴△POA≌△POB≌△POC
∴OA=OB=OC
故O是△ABC外心，正确；
②∵点P到△ABC的三边距离相等，
∴O到三边的距离相等，
∴P点在平面ABC上的射影是△ABC的内心，故正确；
③连接AO并延长交BC于一点E，连接PO，由于PA，PB，PC两两垂直可以得到PA⊥面PBC，而BC?面PBC，∴BC⊥PA，
∵PO⊥平面ABC于O，BC?面ABC，∴PO⊥BC，∴BC⊥平面APE，∵AE?面APE，∴BC⊥AE；
同理可以证明才CH⊥AB，又BH⊥AC．
∴H是△ABC的垂心．
④∠PAO=∠PBO=∠PCO⇒AO=BO=CO⇒O为三角形的外心，正确．
故答案为①③④．

点评 本题考查命题的真假判断与应用，着重考查空间直线与平面、平面与平面平行与垂直的判定与性质，考查空间想象能力，属于中档题．