
���� ��������֪�������������е�ǰ����ɵ�����{an}��ͨ�ʽ��
�����������ĵ�ʽȷ��m��ֵ��
������֪ȡ�������������ڵ���ض�һ����������һ����ż�����������ۼ��ý��ۣ�
��� �⣺��������{an}��������ɵȲ����У�ż����ɵȱ����У������빫�Ⱦ�Ϊ2��
��a5=a1+4��a7=a1+6��a9=a1+8��a4=2a2��a8=8a2��
��a2+a4=a1+a5��a7+a9=a8��
��a2+2a2=a1+4+a1��2a1+14=8a2��
��a1=1��a2=2��
��an=$\left\{\begin{array}{l}{n��nΪ����}\\{{2}^{\frac{n}{2}}��nΪż��}\end{array}\right.$��
����am•am+1•am+2=am+am+1+am+2������
�����������֪����{an}Ϊ��1��2��3��4��5��8��7��16��9����
��m=1ʱ��ʽ�������� 1+2+3=-6=1��2��3����ʽ������
��m=2ʱ��ʽ��������2��3��4��2+3+4����ʽ��������
��m=3��4ʱ��ʽ��������
��m��5ʱ��
��am•am+1•am+2Ϊż����am+am+1+am+2Ϊ������
��ɵ�mȡ����ֵʱ����������
��m=1ʱ������
������������ȡ��s�ż����ȡ��k�����s��k��N*��s��2��k��2��
��Ϊ����{an}���������Ϊ������ż�����Ϊż����
��ˣ�����������ij��˳�ɵȲ����У�
������������ڵ���ض�һ����������һ����ż����
��������������������ż������ÿ��������ż���ĵȲ�����Ϊ������
����������ż����С��������Ϊ2i��2j��2p��1��i��j��p����
��$\frac{2i+2j}{2}$=2i-1+2j-1Ϊ��������i��1��j��2����2j-1Ϊż����2i-1Ϊ����������i=1��
��$\frac{2j+2p}{2}$=2j-1+2p-1Ϊ��������j��2��p��3����2j-1��2p-1��Ϊż����ì�ܣ�
����Ϊk��2������k=2����ż��ֻ�����
�����������3���s+k�����ֵΪ5��
��˵Ȳ�����Ϊd1��d2��d3��d4��d5����d1��d3��d5Ϊ������d2��d4Ϊż������d2=2��
��d1+d3=2d2=4����d1=1��d3=3��������Ϊ1��2��3��4��5��
ͬ�������Ӵ�С���У�������Ϊ5��4��3��2��1��
���ϣ����Ȳ����е��������ʱ����������������Ϊ1��2��3��4��5��5��4��3��2��1��
���� �����ص㿼���˵Ȳ����еĸ���ͻ������ʡ��ȱ����еĸ���ͻ������ʵ�֪ʶ������ؼ���ȷӦ�õȲ�͵ȱ����еĻ�������������⣬�������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��1-\sqrt{2}��\sqrt{2}]$ | B�� | $[1-\sqrt{2}��\sqrt{2}]$ | C�� | $[\frac{1}{2}��\sqrt{2}]$ | D�� | $��\frac{1}{2}��\sqrt{2}]$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
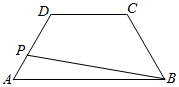 ��ͼ���ڵ�������ABCD�У�AB=8��BC=4��CD=4����P���߶�AD���˶�����|$\overrightarrow{PA}$+$\overrightarrow{PB}$|��ȡֵ��Χ�ǣ�������
��ͼ���ڵ�������ABCD�У�AB=8��BC=4��CD=4����P���߶�AD���˶�����|$\overrightarrow{PA}$+$\overrightarrow{PB}$|��ȡֵ��Χ�ǣ�������| A�� | [6��4+4$\sqrt{3}$] | B�� | [4$\sqrt{2}$��8] | C�� | [4$\sqrt{3}$��8] | D�� | [6��12] |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com