
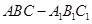 中,
中,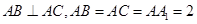 ,点
,点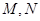 分别为
分别为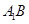 和
和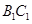 的中点.
的中点.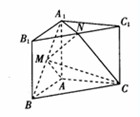
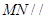 平面
平面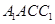 ;
;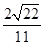 .
.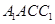 内找到线
内找到线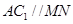 ,从而证明
,从而证明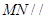 平面
平面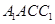 ;第二问,建立空间直角坐标系,写出所有点坐标,先找到平面
;第二问,建立空间直角坐标系,写出所有点坐标,先找到平面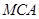 和平面
和平面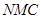 的法向量,利用线面垂直的判定可以确定
的法向量,利用线面垂直的判定可以确定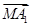 是平面
是平面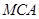 的法向量,而平面
的法向量,而平面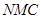 的法向量需要计算求出来,最后利用夹角公式求夹角余弦,注意判断夹角是锐角还是钝角,来判断余弦值的正负.
的法向量需要计算求出来,最后利用夹角公式求夹角余弦,注意判断夹角是锐角还是钝角,来判断余弦值的正负.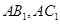
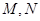 分别为
分别为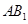 和
和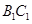 的中点,∴
的中点,∴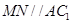 ,
,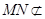 平面
平面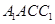 ,
,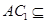 平面
平面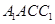 ,
,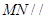 平面
平面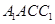 .
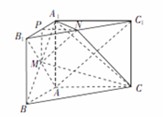
.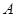 为坐标原点,分别以直线
为坐标原点,分别以直线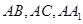 为
为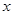 轴,
轴,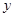 轴,
轴,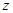 轴,建立空间直角坐标系
轴,建立空间直角坐标系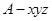 ,如图所示,
,如图所示,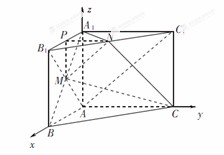
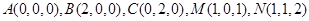 ,
,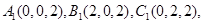
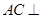 平面
平面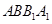 ,∴
,∴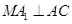 ,∵
,∵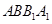 为正方形,∴
为正方形,∴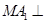 平面
平面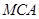 ,
,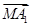 是平面
是平面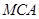 的一个法向量,
的一个法向量,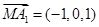 ,设平面
,设平面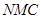 的法向量为
的法向量为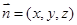 ,
,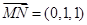 ,
,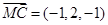 ,
,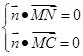 ,
,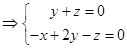
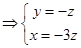 ,令
,令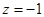 ,
,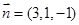 ,
,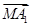 和向量
和向量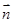 的夹角为
的夹角为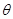 ,则
,则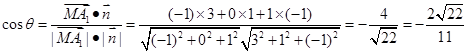 ,
,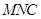 与平面
与平面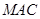 的夹角的余弦值是
的夹角的余弦值是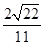 .
.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
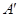 .
.
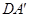 ⊥EF;
⊥EF;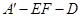 的平面角的余弦值.
的平面角的余弦值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
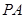 垂直于⊙
垂直于⊙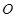 所在的平面,
所在的平面,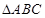 内接于⊙
内接于⊙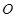 ,且
,且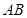 为⊙
为⊙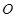 的直径,点
的直径,点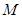 为线段
为线段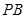 的中点.现有结论:①
的中点.现有结论:①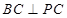 ;②
;② 平面
平面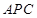 ;③点
;③点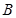 到平面
到平面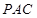 的距离等于线段
的距离等于线段 的长.其中正确的是( )
的长.其中正确的是( )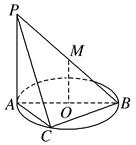
| A.①② | B.①②③ | C.① | D.②③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com