
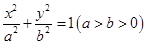 的离心率
的离心率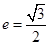 ,且短半轴
,且短半轴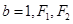 为其左右焦点,
为其左右焦点,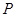 是椭圆上动点.
是椭圆上动点.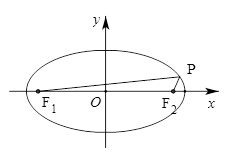
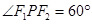 时,求
时,求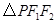 面积;
面积;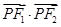 取值范围.
取值范围. 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源:不详 题型:解答题
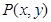 到直线
到直线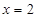 的距离与它到定点
的距离与它到定点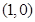 的距离之比为
的距离之比为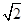 ,并记点
,并记点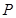 的轨迹为曲线
的轨迹为曲线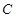 .
.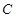 的方程;
的方程;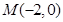 ,过点
,过点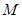 的直线
的直线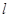 与曲线
与曲线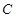 相交于
相交于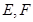 两点,当线段
两点,当线段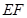 的中点落在由四点
的中点落在由四点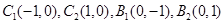 构成的四边形内(包括边界)时,求直线
构成的四边形内(包括边界)时,求直线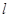 斜率的取值范围.
斜率的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
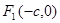 、
、 分别是椭圆
分别是椭圆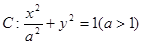 的左、右焦点,
的左、右焦点,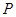 为椭圆
为椭圆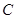 上任意一点,且
上任意一点,且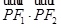 最小值为
最小值为 .
.
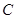 的方程;
的方程;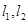 均与椭圆
均与椭圆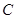 相切,且
相切,且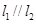 ,试探究在
,试探究在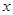 轴上是否存在定点
轴上是否存在定点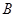 ,点
,点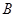 到
到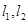 的距离之积恒为1?若存在,请求出点
的距离之积恒为1?若存在,请求出点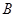 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
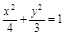 上有n个不同的点:P1,P2, ,Pn,椭圆的右焦点为F,数列{|PnF|}是公差大于
上有n个不同的点:P1,P2, ,Pn,椭圆的右焦点为F,数列{|PnF|}是公差大于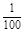 的等差数列,则n的最大值是 ( )
的等差数列,则n的最大值是 ( )| A.198 | B.199 |
| C.200 | D.201 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
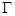 的方程为
的方程为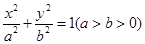 ,点P的坐标为(-a,b).
,点P的坐标为(-a,b).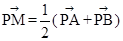 ,求点
,求点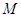 的坐标;
的坐标;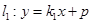 交椭圆
交椭圆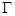 于
于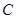 、
、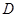 两点,交直线
两点,交直线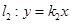 于点
于点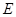 .若
.若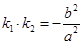 ,证明:
,证明: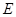 为
为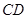 的中点;
的中点;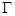 上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆
上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆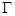 上存在不同的两个交点
上存在不同的两个交点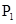 、
、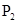 满足
满足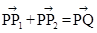 ,写出求作点
,写出求作点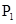 、
、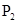 的步骤,并求出使
的步骤,并求出使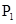 、
、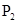 存在的θ的取值范围.
存在的θ的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
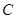 的中心为坐标原点
的中心为坐标原点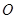 ,一个长轴端点为
,一个长轴端点为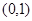 ,短轴端点和焦点所组成的四边形为正方形,若直线
,短轴端点和焦点所组成的四边形为正方形,若直线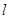 与
与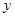 轴交于点
轴交于点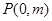 ,与椭圆
,与椭圆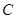 交于不同的两点
交于不同的两点 ,且
,且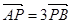 。(14分)
。(14分)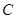 的方程;
的方程;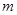 的取值范围。
的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
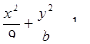 的右焦点F2重合,F1是椭圆的左焦点;
的右焦点F2重合,F1是椭圆的左焦点;  ABC中,若A(-4,0),B(0,-3),点C在抛物线y2=4x上运动,求
ABC中,若A(-4,0),B(0,-3),点C在抛物线y2=4x上运动,求 ABC重心G的轨迹方程;
ABC重心G的轨迹方程;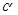 ,∠PF2F1=
,∠PF2F1=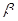 ,求cos
,求cos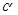
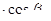 的值及
的值及 PF1F2的面积。
PF1F2的面积。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com