△ABC中,角A、B、C所对的边a,b,c成等差数列,且最大角是最小角的2倍,则 cosA+cosC= .
【答案】
分析:由题意可得 2b=a+c,设C为最大角,则A为最小角,可得C=2A,且 0<A<
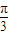
.再由正弦定理可得2sin3A=sinA+sin2A,
化简可得 2cosA=5-8sin
2A=5-8(1-cos
2A ),解得cosA 的值,即可得到cosA+cosC的值.
解答:解:△ABC中,角A、B、C所对的边a,b,c成等差数列,∴2b=a+c.
设C为最大角,则A为最小角,再由最大角是最小角的2倍,可得C=2A,且 0<A<
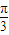
.
再由正弦定理可得 2sinB=sinA+sin2A,∴2sin(π-3A)=sinA+sin2A,即2sin3A=sinA+sin2A,
2(3sinA-4sin
3A)=sinA+2sinAcosA,化简可得 2cosA=5-8sin
2A=5-8(1-cos
2A ),
解得cosA=

,cosA=-

(舍去).
则 cosA+cosC=cosA+cos2A=cosA+2cos
2A-1=

+2×
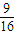
-1=

,
故答案为

.
点评:本题主要考查等比数列的定义和性质,正弦定理、倍角公式的应用,属于中档题.

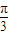 .再由正弦定理可得2sin3A=sinA+sin2A,
.再由正弦定理可得2sin3A=sinA+sin2A,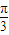 .
. ,cosA=-
,cosA=- (舍去).
(舍去). +2×
+2×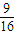 -1=
-1= ,
, .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案