
分析 根据题意,分析可得要“确保6号、15号与24号同时入选并被分配到同一地点”,则除6、15、24号之外的另外三人的编号必须都大于25或都小于6号,则先分另外三人的编号必须“都大于25”或“都小于6号”这2种情况讨论选出其他三人的情况,再将选出2组进行全排列,对应实验校区、南山本部;由分步计数原理计算可得答案.
解答 解:根据题意,要“确保6号、15号与24号同时入选并被分配到同一地点”,则除6、15、24号之外的另外一组三人的编号必须都大于25或都小于6号,
则分2种情况讨论选出的情况:
①、如果另外三人的编号都大于25,则需要在编号为25、26、27、28、29、30的6人中,任取3人即可,有C63=20种情况,
②、如果另外三人的编号都小于6,则需要在编号为1、2、3、4、5的5人中,任取3人即可,有C53=10种情况,
选出剩下3人有20+10=30种情况,
再将选出的2组进行全排列,对应实验校区、南山本部,有A22=2种情况,
则“确保6号、15号与24号同时入选并被分配到同一地点”的选取种数为30×2=60种;
故答案为:60.
点评 本题考查排列组合的应用,解题的关键是分析如何“确保6号、15号与24号同时入选并被分配到同一地点”,进而确定分步、分类讨论的依据.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:选择题
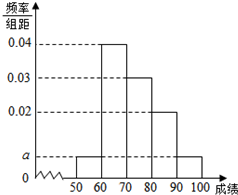 某校100名学生数学竞赛成绩的频率分布直方图如图所示,成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100],则该次数学成绩在[50,60)内的人数为( )
某校100名学生数学竞赛成绩的频率分布直方图如图所示,成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100],则该次数学成绩在[50,60)内的人数为( )| A. | 20 | B. | 15 | C. | 10 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 合计 | |
| 甲 | 20 | 5 | 25 |
| 乙 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com