
分析 (1)求出导函数,通过当a≤0时,当a>0时,判断导函数的符号,然后判断函数的单调性.
(2)通过当a=0时,当a<0时,当a>0时,分别求解判断求解函数的最小值,推出a的取值范围.
解答 解:(1)$f'(x)=1-\frac{a}{x}=\frac{x-a}{x}$,…(1分)
当a≤0时,∵x>0,∴f'(x)>0恒成立,
∴f(x)在定义域(0,+∞)上单调递增…(3分)
当a>0时,令f'(x)=0,得x=a,
∵x>0,∴f'(x)>0得x>a;f'(x)<0得0<x<a,
∴f(x)在(0,a)上单调递减,
在(a,+∞)上单调递增.…(5分)
(2)当a=0时,f(x)>0恒成立…(6分)
当a<0时,当x→0时,f(x)→-∞,f(x)≥0不成立…(8分)
当a>0时,由(1)可知f(x)min=f(a)=a-alna,由f(a)=a-alna≥0
得1-lna≥0,∴a∈(0,e]…(11分)
综上所述,a的取值范围是[0,e].…(12分)
点评 本题考查函数的单调性的判断与应用,导数的应用,考查分类讨论思想以及转化思想的应用.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{7}{48}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
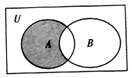 若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )
若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )| A. | ∁U(A∩B) | B. | ∁U(A∪B) | C. | A∩(∁UB) | D. | (∁UA)∩B |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com