
分析 (1)结合一元二次函数的图形特征,列出-$\frac{b}{2a}$=$\frac{1}{2}$与△=0;
(2)根据对称轴与区间的关系来分类讨论;
(3)观察图形知2n$≤\frac{1}{4}$⇒n$≤\frac{1}{8}$; f(x)在[m,n]上单调递增 $\left\{\begin{array}{l}{f(m)=2m}\\{f(n)=2n}\end{array}\right.$⇒$\left\{\begin{array}{l}{-{m}^{2}+m=2m}\\{-{n}^{2}+n=2n}\end{array}\right.$
解答 解:(1)由题意知f(x)=ax2+bx关于x=$\frac{1}{2}$对称
∴-$\frac{b}{2a}$=$\frac{1}{2}$
ax2+bx=x有两个相等的实根,∴△=0
∴$\left\{\begin{array}{l}{a=-1}\\{b=1}\end{array}\right.$
所以,f(x)=-x2+x;
(2)F(x)=kx+1+x2-x=x2+(k-1)x+1
F(x)的对称轴为:x=-$\frac{k-1}{2}$
①当-$\frac{k-1}{2}$≤1时,F(x)min=F(1)≤k+1
②当 1<-$\frac{k-1}{2}$≤2时,$F(x)_{min}=1-\frac{(k-1)^{2}}{4}$
③当-$\frac{k-1}{2}$>2 时,F(x)min=F(2)=2k+3
∴F(x)min=$\left\{\begin{array}{l}{k+1,k≥-1}\\{1-\frac{(k-1)^{2}}{4},-3≤k<-1}\\{2k+3,k<-3}\end{array}\right.$
(3)f(x)=-x2+x=-(x-$\frac{1}{2}$)2+$\frac{1}{4}$
∴2n$≤\frac{1}{4}$⇒n$≤\frac{1}{8}$
∴f(x)在[m,n]上单调递增
∴$\left\{\begin{array}{l}{f(m)=2m}\\{f(n)=2n}\end{array}\right.$⇒$\left\{\begin{array}{l}{-{m}^{2}+m=2m}\\{-{n}^{2}+n=2n}\end{array}\right.$
∵m<n
∴$\left\{\begin{array}{l}{m=-1}\\{n=0}\end{array}\right.$
点评 本题主要考查了一元二次函数的性质,分类讨论区间与对称轴的关系,属中等题.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(0,2) | B. | (-2,0)∪(0,2) | C. | (-2,0)∪(2,+∞) | D. | (-∞,-2)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{3}{2},4}]$ | B. | $[{2,\frac{9}{2}}]$ | C. | [-11,-1] | D. | [-3,7] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
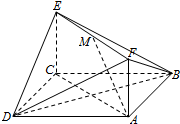 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,$AB=\sqrt{2}$,AF=1,M是线段EF的中点.
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,$AB=\sqrt{2}$,AF=1,M是线段EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{S}_{7}}{{a}_{7}}$ | B. | $\frac{{S}_{6}}{{a}_{6}}$ | C. | $\frac{{S}_{9}}{{a}_{9}}$ | D. | $\frac{{S}_{8}}{{a}_{8}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com