
| 3 |
| 3 |
| x02-x12 |
| 4 |
| y02-y12 |
| x02-x12 |
| 1 |
| 4 |
| 3 |
| x2 |
| 4 |
(
|
| 3 |
| 3 |
| 3 |
| x2 |
| 4 |
| x2 |
| 4 |
| x02 |
| 4 |
| x12 |
| 4 |
| x02-x12 |
| 4 |
| y0-y1 |
| x0-x1 |
| y0+y1 |
| x0+x1 |
| y02-y12 |
| x02-x12 |
| 1 |
| 4 |
| 3 |
| x2 |
| 4 |
| 3 |
|
| (x3-x4)2+(y3-y4)2 |
| (1+m2)[(y3+y4)2-4y3y4] |
| 4(1+m2) |
| 4+m2 |
2
| ||
|
| 1+m2 |
| 1 |
| 2 |
| 3 |
| ||
| 4+m2 |
4
| ||
| t2+3 |
4
| ||
t+
|
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |



| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º
A¡¢
| ||
B¡¢
| ||
C¡¢
| ||
D¡¢
|
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º
|
| A¡¢£¨0£¬1] |
| B¡¢£¨-¡̃£¬1] |
| C¡¢£¨-1£¬1] |
| D¡¢£¨1£¬2£© |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º
 Èçͼ1£¬¡÷ABCΪƠưÈư½ÇĐΣ¬¡÷BCDΪµÈÑüÖ±½ÇÈư½ÇĐΣ¬¡ÏBCD=90¡ă£¬½«¡÷ABCÑØBC±ßƠÛµ₫µ½¡÷A¡äBCµÄλÖĂ£¬Ê¹A¡äB=A¡äD£¬EΪBDÖĐµă£¬Èçͼ2£®
Èçͼ1£¬¡÷ABCΪƠưÈư½ÇĐΣ¬¡÷BCDΪµÈÑüÖ±½ÇÈư½ÇĐΣ¬¡ÏBCD=90¡ă£¬½«¡÷ABCÑØBC±ßƠÛµ₫µ½¡÷A¡äBCµÄλÖĂ£¬Ê¹A¡äB=A¡äD£¬EΪBDÖĐµă£¬Èçͼ2£®²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º
| ÄêÁ䣨Ë꣩ | [15£¬25£© | [25£¬35£© | [35£¬45£© | [45£¬55£© | [55£¬65£© | [65£¬75] |
| ƵÊư | 5 | 10 | 15 | 10 | 5 | 5 |
| Ỗ³ÉÈËÊư | 4 | 6 | 9 | 6 | 3 | 4 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º
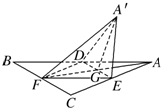 Èçͼ£¬ƠưÈư½ÇĐÎABCµÄÖĐÏßAFÓëÖĐλÏßDEÏཻÓÚµăG£¬̉ÑÖª¡÷A¡äEDÊÇ¡÷AEDÈÆDEĐưת¹ư³̀ÖеÄ̉»¸öͼĐΣ¬ÏÖ¸ø³öÏÂÁĐËĸöĂǜ⣺
Èçͼ£¬ƠưÈư½ÇĐÎABCµÄÖĐÏßAFÓëÖĐλÏßDEÏཻÓÚµăG£¬̉ÑÖª¡÷A¡äEDÊÇ¡÷AEDÈÆDEĐưת¹ư³̀ÖеÄ̉»¸öͼĐΣ¬ÏÖ¸ø³öÏÂÁĐËĸöĂǜ⣺²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 11 |

| A¡¢i£¼12 | B¡¢i£¾11 |
| C¡¢i£¼11 | D¡¢i¡Ü6 |
²é¿´´đ°¸ºÍ½âÎö>>
¹ú¼ÊÑ§Đ£ÓÅÑ¡ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com