
分析 先求出平面ABC的法向量,再利用法向量的夹角公式即可得出.
解答 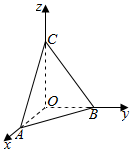 解:∵A(1,0,0),B(0,2,0),C(0,0,3),
解:∵A(1,0,0),B(0,2,0),C(0,0,3),
∴$\overrightarrow{AB}=(-1,2,0)$,$\overrightarrow{AC}=(-1,0,3)$.
设平面ABC的法向量为$\overrightarrow{n}=(x,y,z)$,则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=-x+2y=0}\\{\overrightarrow{n}•\overrightarrow{AC}=-x+3z=0}\end{array}\right.$,
令x=2,则y=1,z=$\frac{2}{3}$.∴$\overrightarrow{n}=(2,1,\frac{2}{3})$.
①取平面xoy的法向量$\overrightarrow{m}=(0,0,1)$.
则$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|\;|\overrightarrow{n}|}$=$\frac{\frac{2}{3}}{1×\sqrt{{2}^{2}+1+(\frac{2}{3})^{2}}}$=$\frac{2}{7}$.
则平面x0y与平面ABC夹角的余弦为$\frac{2}{7}$.
②设平面xoz的法向量$\overrightarrow{m}$=(0,1,0).
则$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|\;|\overrightarrow{n}|}$=$\frac{1}{1×\sqrt{{2}^{2}+1+(\frac{2}{3})^{2}}}$=$\frac{3}{7}$.
则平面x0z与平面ABC夹角的余弦为$\frac{3}{7}$.
③设平面yoz的法向量$\overrightarrow{m}$=(1,0,0).
则$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|\;|\overrightarrow{n}|}$=$\frac{2}{1×\sqrt{{2}^{2}+1+(\frac{2}{3})^{2}}}$=$\frac{6}{7}$.
则平面y0z与平面ABC夹角的余弦为$\frac{6}{7}$.
点评 本题主要考查二面角的计算,利用向量法是解决二面角的常用方法,熟练掌握利用二面角的两个半平面的法向量的夹角公式求得二面角是解题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2<b2 | B. | $\frac{a}{b}<1$ | C. | a<1-b | D. | $\frac{1}{a}<\frac{1}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
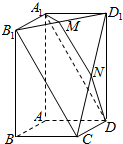 如图所示,多面体A1B1D1DCBA是长方体A1B1C1D-ABCD被平面B1CD1截去一个三棱锥后所得的几何体,M为B1D1的中点,过A1、D、M的平面交CD1于点N.
如图所示,多面体A1B1D1DCBA是长方体A1B1C1D-ABCD被平面B1CD1截去一个三棱锥后所得的几何体,M为B1D1的中点,过A1、D、M的平面交CD1于点N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在某批次的某种灯泡中,随机地抽取500个样品,并对其寿命进行追踪调查,将结果列成频率分布直方图如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于500天的灯泡是优等品,寿命小于300天的灯泡是次品,其余的灯泡是正品.
在某批次的某种灯泡中,随机地抽取500个样品,并对其寿命进行追踪调查,将结果列成频率分布直方图如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于500天的灯泡是优等品,寿命小于300天的灯泡是次品,其余的灯泡是正品.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 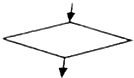 | B. | 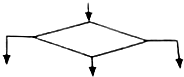 | ||
| C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com