Question

10．如图，在矩形ABCD中，AB=8，BC=4，E为DC边的中点，沿AE将△ADE折起，在折起过程中，下列结论中能成立的序号为④．

①ED⊥平面ACD
②CD⊥平面BED
③BD⊥平面ACD
④AD⊥平面BED．

Answer 1

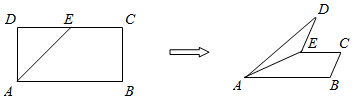
分析 在折起过程中，画出D点在平面BCE上的投影轨迹，利用线面垂直的判定定理即可逐项判断得解．

解答 解：∵在矩形ABCD中，AB=8，BC=4，E为DC边的中点
∴在折起过程中，D点在平面BCE上的投影如右图．
∵DE与AC所成角不能为直角，
∴DE不会垂直于平面ACD，故①错误；
只有D点投影位于O₂位置时，即平面AED与平面AEB重合时，
才有BE⊥CD，此时CD不垂直于平面AEBC，
故CD与平面BED不垂直，故②错误；
BD与AC所成角不能成直线，
∴BD不能垂直于平面ACD，故③错误；
∵AD⊥ED，并且在折起过程中，有AD⊥BC，
∴存在一个位置使AD⊥BE，
∴在折起过程中AD⊥平面BED，故④正确．
故答案为：④．

点评 本题考查命题真假的判断，是中档题，解题时要认真审题，注意线面垂直的判定定理的合理运用．