
 �����Ƿ��������B��A��B��
�����Ƿ��������B��A��B��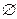 ������������������ʵ��x��ֻҪn��2������gn(x)��0.
������������������ʵ��x��ֻҪn��2������gn(x)��0. 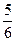 ��3��ֻҪn��2,n��N������gn(x)��0
��3��ֻҪn��2,n��N������gn(x)��0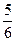
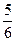 .
.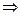 x��0��x��1.
x��0��x��1. 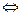 f��gn�C1(x)�ݣ�0
f��gn�C1(x)�ݣ�0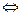 gn�C1(x)��0��gn�C1(x)��1
gn�C1(x)��0��gn�C1(x)��1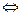 6x�C6x2��0
6x�C6x2��0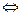 x��0��x��1
x��0��x��1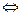 6x�C6x2��1
6x�C6x2��1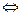
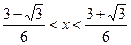
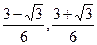 )��(1,+��)�ڵ�����ʵ��x,
)��(1,+��)�ڵ�����ʵ��x,


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
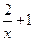 ��=lgx����f��x����
��=lgx����f��x����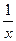 ��=3x����f��x��.
��=3x����f��x��.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
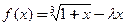 ������
������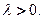
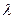 ��ȡֵ��Χ��ʹ�ú���
��ȡֵ��Χ��ʹ�ú���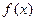 ��
��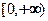 ���ǵ����ݼ�������
���ǵ����ݼ�������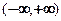 �ϣ�
�ϣ�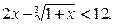
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
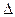 ABP���ΪS.��1������S=f(x)�Ľ���ʽ���������ֵ��2����f[f(3)]��ֵ��
ABP���ΪS.��1������S=f(x)�Ľ���ʽ���������ֵ��2����f[f(3)]��ֵ��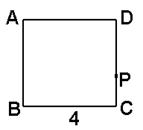
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
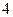 �·ݣ���һ�¿��װͶ��ij�̳����ۣ�
�·ݣ���һ�¿��װͶ��ij�̳����ۣ�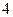 ��
��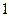 �ոÿ��װ�����۳�
�ոÿ��װ�����۳�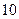 �����ڶ����۳�
�����ڶ����۳�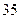 ��������������
��������������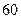 ����Ȼ��ÿ���۳��ļ����ֱ����
����Ȼ��ÿ���۳��ļ����ֱ����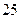 ����ֱ�����������ﵽ����ÿ�����۵ļ����ֱ�ݼ�
����ֱ�����������ﵽ����ÿ�����۵ļ����ֱ�ݼ�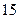 �������µ÷�װ�����۳�
�������µ÷�װ�����۳�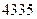 ����������
����������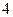 �¼��Ÿÿ��װ���ۼ�����ࣿ�����ֵ�Ƕ��٣��������ɣ������̳����۴˷�װ����
�¼��Ÿÿ��װ���ۼ�����ࣿ�����ֵ�Ƕ��٣��������ɣ������̳����۴˷�װ����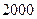 ��ʱ������Ͼ����У����������������½���������
��ʱ������Ͼ����У����������������½���������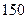 ��ʱ����������ʧ���ʸÿ��װ������������Ƿ�
��ʱ����������ʧ���ʸÿ��װ������������Ƿ� �죿��˵�����ɡ�
�죿��˵�����ɡ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
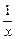 (x�ܣ�
(x�ܣ�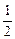 )��ֵ����( )
)��ֵ����( )A��(����,��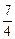 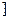 | B���ۣ�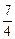 ,+�� ,+��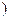 | C����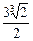 ,+�� ,+��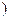 | D��(����,��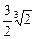 �� �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
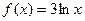 ����
����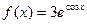 ����
����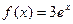 ����
����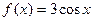 .�����
.���ж���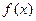 �������ڵ�����һ���Ա���
�������ڵ�����һ���Ա���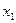 ������Ψһ���Ա���
������Ψһ���Ա���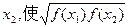 =3�����ĺ����ǣ� ��.
=3�����ĺ����ǣ� ��.| A���� | B���ڢ� | C���٢ڢ� | D���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com