
分析 根据正切函数的定义、图象与性质,求出函数f(x)的周期、定义域和单调减区间.
解答 解:函数y=-tan($\frac{π}{2}$x-$\frac{π}{6}$),
∴f(x)的周期为:$T=\frac{π}{{\frac{π}{2}}}=2$;…(2分)
要使函数解析式有意义,必须
$\frac{π}{2}x-\frac{π}{6}≠kπ+\frac{π}{2},k∈Z$,…(4分)
即$\frac{π}{2}x≠kπ+\frac{2π}{3},k∈Z$,
解得$x≠2k+\frac{4}{3},k∈Z$;
∴f(x)的定义域为:$\left\{{x\left|{x≠2k+\frac{4}{3},k∈Z}\right.}\right\}$;…(6分)
函数值y随着x的增加而减小,函数f(x)只有减区间无增区间,
令$kπ-\frac{π}{2}<\frac{π}{2}x-\frac{π}{6}<kπ+\frac{π}{2},k∈Z$; …(8分)
得$kπ-\frac{π}{3}<\frac{π}{2}x<kπ+\frac{2π}{3},k∈Z$,
得:$2k-\frac{2}{3}<x<2k+\frac{4}{3},k∈Z$,
∴函数f(x)的减区间为:$(2k-\frac{2}{3},2k+\frac{4}{3}),k∈Z$.…(10分)
点评 本题考查了正切函数的定义、图象与性质的应用问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin(α+β)=sinαcosβ+cosαsinβ | B. | sin(α-β)=cosβsinα-sinβcosα | ||
| C. | cos(α-β)=cosαcosβ-sinαsinβ | D. | cos(α+β)=cosαcosβ-sinαsinβ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $-\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 评分等级 | ☆ | ☆☆ | ☆☆☆ | ☆☆☆☆ | ☆☆☆☆☆ |
| 小学 | 2 | 7 | 9 | 20 | 12 |
| 中学 | 3 | 9 | 18 | 12 | 8 |
| 学校类型 | 满意 | 不满意 | 总计 |
| 小学 | 50 | ||
| 中学 | 50 | ||
| 总计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
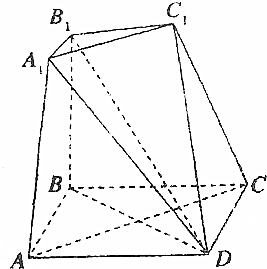 如图所示的七面体是由三棱台ABC-A1B1C1和四棱锥D-AA1C1C对接而成,四边形ABCD是边长为2的正方形,BB1⊥平面⊥ABCD,BB1=2A1B1=2.
如图所示的七面体是由三棱台ABC-A1B1C1和四棱锥D-AA1C1C对接而成,四边形ABCD是边长为2的正方形,BB1⊥平面⊥ABCD,BB1=2A1B1=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com