
分析 分类讨论,即可确定实数m的取值范围.
解答 解:1、当x<0时,f(f(x)=(-x+m)2-1,图象为开口向上的抛物线的在y轴左侧的部分,顶点为(0,m2-1)
2、当0≤x<1时,f(f(x)=-x2+1+m,图象为开口向下的抛物线在0≤x<1之间的部分,顶点为(0,m+1).根据题意m>0,所以m+1>1
3、当x≥1时,f(f(x)=(x2-1)2-1,图象为开口向上的抛物线在x=1右侧的部分,顶点为(1,-1)
根据题意,函数y=f(f(x)-1有3个不同的零点,即f(f(x)的图象与y=1有3个不同的交点.
根据以上分析的3种情况,第2及第3种情况的图象分别与y=1有不同的2个交点,所以只需要第1种情况与y=1有1个交点即可,所以只要m2-1<1即可,解得m<$\sqrt{2}$.再根据题意m>0可得m的取值范围为(0,$\sqrt{2}$)
故答案为(0,$\sqrt{2}$).
点评 本题考查函数的零点,考查分段函数的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
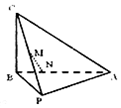 如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB.
如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,2,3} | B. | {-2,1,2,3} | C. | {-1,0,2,3} | D. | {2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
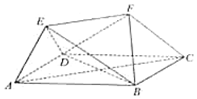 如图,在多面体ABCDEF中,底面ABCD是菱形,AB=2,∠DAB=60°,EF∥AC,EF=$\sqrt{3}$.
如图,在多面体ABCDEF中,底面ABCD是菱形,AB=2,∠DAB=60°,EF∥AC,EF=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在正方体ABCD-A1B1C1D1中,棱AB的中点为P,若光线从点P出发,依次经三个侧面BCC1B1,DCC1D1,ADD1A1反射后,落到侧面ABB1A1(不包括边界),则入射光线PQ与侧面BCC1B1所成角的正切值的范围是( )
如图,在正方体ABCD-A1B1C1D1中,棱AB的中点为P,若光线从点P出发,依次经三个侧面BCC1B1,DCC1D1,ADD1A1反射后,落到侧面ABB1A1(不包括边界),则入射光线PQ与侧面BCC1B1所成角的正切值的范围是( )| A. | ($\frac{3}{4}$,$\frac{5}{4}$) | B. | ($\frac{2\sqrt{17}}{17}$,4) | C. | ($\frac{\sqrt{5}}{5}$,$\frac{3}{2}$) | D. | ($\frac{3\sqrt{5}}{10}$,$\frac{5}{4}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com