
分析 将问题转化为一般问题:设n≥3,从A={a1,a2,a3,…an},B={b1,b2,b3,…bn},C={c1,c2,c3,…cn},D={d1,d2,d3,…dn},这四个数列中选取n个项,且满足:①1,2,…,每个下标都出现;②下标相邻的任两项不在同一个数列中(下标n与1视为相邻),其选取方法数记为xn,今确定xn的运算式即可.
解答 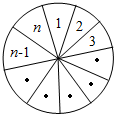 解:先一般化为下述问题:设n≥3,从A={a1,a2,a3,…an},B={b1,b2,b3,…bn},C={c1,c2,c3,…cn},D={d1,d2,d3,…dn},
解:先一般化为下述问题:设n≥3,从A={a1,a2,a3,…an},B={b1,b2,b3,…bn},C={c1,c2,c3,…cn},D={d1,d2,d3,…dn},
这四个数列中选取n个项,且满足:
①1,2,…,每个下标都出现;
②下标相邻的任两项不在同一个数列中(下标n与1视为相邻),其选取方法数记为xn,今确定xn的运算式;
将一个圆盘分成n个扇形格,顺次编号为1,2…,并将数列A,B,C,D,各染一种颜色,对于任一个选项方案,如果下标为i的项取自某颜色数列,则将第i号扇形格染上该颜色,
于是xn就成为将圆盘的n个扇形格染四色,使相邻格不同色的染色方法数,易知,x1=4,x2=12,
xn+xn-1=4•3n-1,(n≥3),(1)
将(1)写作(-1)nxn-(-1)n-1xn-1=-4•(-3)n-1,
因此(-1)n-1xn-(-1)n-2xn-1=-4•(-3)n-2,
…
(-1)3x3-(-1)2x2=-4•(-3)2,
(-1)2x2=-4•(-3),
相加得(-1)nxn=3+(-3)n,
于是xn=3n+3•(-1)n,(n≥2),
当n=13时,x13=313-3.
点评 本题主要考查与数列有关的计算问题,根据条件构造数列,利用累加法是解决本题的关键.综合性较强,难度较大,是一个难度较大的竞赛试题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com