
| A�� | $\frac{n��n+1��}{2}$ | B�� | 22n-1+2n-1 | C�� | $\frac{��1+{2}^{n}��^{2}}{2}$ | D�� | 2n-1 |
���� ����f��x��=$\left\{\begin{array}{l}{{2}^{x}-1��0��x��1��}\\{f��x-1��+m��x��1��}\end{array}\right.$�ڶ�����[0��+�ޣ��ϵ�����������������a��0������f��x��=a����ֻ��һ��ʵ���⣬�ɵú���f��x��=$\left\{\begin{array}{l}{{2}^{x}-1��0��x��1��}\\{f��x-1��+m��x��1��}\end{array}\right.$�ڶ�����[0��+�ޣ��ϵ�����������ͼ����������m=1
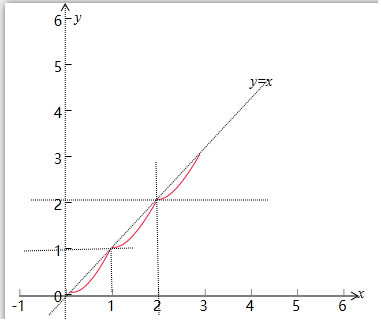
��ͼ�����£�����g��x��=f��x��-x������[0��2n]��n��N*�����������ֱ�Ϊ0��1��2��3����2n�����ݵȲ������ʽ��⣮
���  �⣺�ߺ���f��x��=$\left\{\begin{array}{l}{{2}^{x}-1��0��x��1��}\\{f��x-1��+m��x��1��}\end{array}\right.$�ڶ�����[0��+�ޣ��ϵ�����������m��1��
�⣺�ߺ���f��x��=$\left\{\begin{array}{l}{{2}^{x}-1��0��x��1��}\\{f��x-1��+m��x��1��}\end{array}\right.$�ڶ�����[0��+�ޣ��ϵ�����������m��1��
����Ϊ��������a��0������f��x��=a����ֻ��һ��ʵ���⣬�ߺ���f��x��=$\left\{\begin{array}{l}{{2}^{x}-1��0��x��1��}\\{f��x-1��+m��x��1��}\end{array}\right.$�ڶ�����[0��+�ޣ��ϵ�����������ͼ������������m=1
��ͼ�����£�����g��x��=f��x��-x������[0��2n]��n��N*�����������ֱ�Ϊ0��1��2��3����2n��
���������ĺ͵���$\frac{{2}^{n}��1+{2}^{n}��}{2}={2}^{n-1}+{2}^{2n-1}$��
��ѡ��B��
���� ���⿼�麯������㣬��Ȿ�⣬�ؼ����о�������f��x�����ʣ�������ͼ������y=g��x��������[0��2n]��n��N*���ϵ�������������ת��Ϊ����������⣬�����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{3}$ | B�� | $\frac{2}{5}$ | C�� | $\frac{3}{5}$ | D�� | $\frac{4}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [10��+�ޣ� | B�� | ��-�ޣ�2] | C�� | ��-�ޣ�2]��[10��+�ޣ� | D�� | ��-�ޣ�1]��[5��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | ��ѧ | |||
| ���� | ���� | ���� | ||
| ���� | ���� | 7 | 20 | 5 |
| ���� | 9 | 18 | 6 | |
| ���� | a | 4 | b | |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ֱ�������� | B�� | ��������� | C�� | ���������� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{7}{2}$ | B�� | $\frac{7}{2}$ | C�� | $-\frac{9}{2}$ | D�� | $\frac{9}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com