
已知函数 在
在 时取得最大值4.
时取得最大值4.
(1)求 的最小正周期;
的最小正周期;
(2)求 的解析式;
的解析式;
(3)若 ,求
,求 的值域.
的值域.
 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:解答题
设函数 .
. 为常数且
为常数且
(1)当 时,求
时,求 ;
;
(2)若 满足
满足 ,但
,但 ,则称
,则称 为
为 的二阶周期点.证明函数
的二阶周期点.证明函数 有且仅有两个二阶周期点,并求二阶周期点
有且仅有两个二阶周期点,并求二阶周期点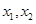 ;
;
(3)对于(2)中的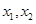 ,设
,设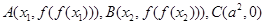 ,记
,记 的面积为
的面积为 ,求
,求 在区间
在区间 上的最大值和最小值。
上的最大值和最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
二次函数f(x)满足f(x+1)-f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)在区间[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,求实数m的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某通讯公司需要在三角形地带 区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域
区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域 内,乙中转站建在区域
内,乙中转站建在区域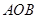 内.分界线
内.分界线 固定,且
固定,且 =
= 百米,边界线
百米,边界线 始终过点
始终过点 ,边界线
,边界线 满足
满足 .
.
设 (
( )百米,
)百米,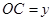 百米.
百米.
(1)试将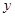 表示成
表示成 的函数,并求出函数
的函数,并求出函数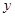 的解析式;
的解析式;
(2)当 取何值时?整个中转站的占地面积
取何值时?整个中转站的占地面积 最小,并求出其面积的最小值.
最小,并求出其面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
定义在 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数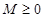 ,都有
,都有 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的一个上界.已知函数
的一个上界.已知函数 ,
, .
.
(1)若函数 为奇函数,求实数
为奇函数,求实数 的值;
的值;
(2)在(1)的条件下,求函数 在区间
在区间 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数 在
在 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=2x- ,x∈(0,1].
,x∈(0,1].
(1)当a=-1时,求函数y=f(x)的值域;
(2)若函数y=f(x)在x∈(0,1]上是减函数,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com