若方程2ax2－x－1＝0在(0,1)内恰有一解，则a的取值范围为( )
A．a<－1 B．a>1
C．－1<a<1 D．0≤a<1
科目：高中数学 来源： 题型：
已知f(x)＝3x，并且f(a＋2)＝18，g(x)＝3ax－4x的定义域为[－1,1]．
(1)求函数g(x)的解析式；
(2)判断g(x)的单调性；
(3)若方程g(x)＝m有解，求m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
如果函数f(x)＝x2＋bx＋c对任意的实数x都有f(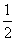
＋x)＝f(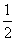－x)，那么( )
A．f(－2)<f(0)<f(2) B．f(0)<f(－2)<f(2)
C．f(2)<f(0)<f(－2) D．f(0)<f(2)<f(－2)
查看答案和解析>>
科目：高中数学 来源： 题型：
已知函数f(x)＝x2－2(a＋2)x＋a2，g(x)＝－x2＋2(a－2)x－a2＋8，设H1(x)＝max{f(x)，g(x)}，H2(x)＝min{f(x)，g(x)}(max{p，q}表示p，q中的较大值，min{p，q}表示p，q中的较小值)．记H1(x)的最小值为A，H2(x)的最大值为B，则A－B＝( )
A．16 B．－16
C．a2－2a－16 D．a2＋2a－16
查看答案和解析>>
科目：高中数学 来源： 题型：
若a<b<c，则函数f(x)＝(x－a)(x－b)＋(x－b)(x－c)＋(x－c)(x－a)的两个零点分别位于区间( )
A．(a，b)和(b，c)内
B．(－∞，a)和(a，b)内
C．(b，c)和(c，＋∞)内
D．(－∞，a)和(c，＋∞)内
查看答案和解析>>
科目：高中数学 来源： 题型：
为了保证信息安全，传输必须使用加密方式，有一种方式其加密、解密原理如下：
已知加密为y＝ax－2(x为明文，y为密文)，如果明文“3”通过加密后得到密文为“6”，再发送，接受方通过解密得到明文“3”，若接受方接到密文为“14”，则原发的明文是________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
)(x≠0)，且cosα＝
x.求sinα＋
的值．