
【题目】设Sn是数列{an}的前n项和. (Ⅰ)若2Sn=3n+3.求{an}的通项公式;
(Ⅱ)若a1=1,an+1﹣an=2n(n∈N*),求Sn .
【答案】解:(Ⅰ)∵2Sn=3n+3, ∴当n=1时,2a1=3+3,解得a1=3.
当n≥2时,2Sn﹣1=3n﹣1+3,
可得2an=3n﹣3n﹣1 , 解得an=3n﹣1 .
∴an= ![]() .
.
(Ⅱ)∵an+1﹣an=2n(n∈N*),
∴an=(an﹣an﹣1)+(an﹣1﹣an﹣2)+…+(a2﹣a1)+a1
=2n﹣1+2n﹣2+…+2+1= ![]() =2n﹣1,
=2n﹣1,
∴Sn=(21﹣1)+(22﹣1)+…+(2n﹣1)=(21+22+…+2n)﹣n= ![]() ﹣n=2n+1﹣n﹣2
﹣n=2n+1﹣n﹣2
【解析】(1)利用递推关系即可得出.(Ⅱ)利用“累加求和”可得an , 再求出数列的前n项和.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系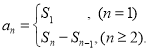 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=sin(x﹣30°)+cos(x﹣60°),g(x)=2sin2 ![]() .
.
(1)若α为第一象限角且f(α)= ![]() ,求g(α)之值;
,求g(α)之值;
(2)求f(x﹣1080°)≥g(x)在[0,360°]内的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取![]() 名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:
名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图: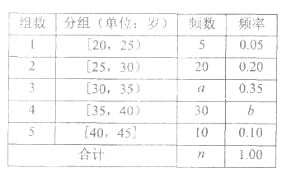
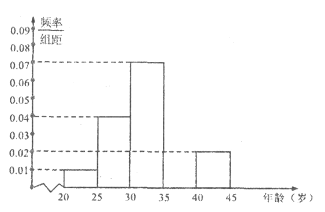
(1)求出表中的![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)媒体记者为了做好调查工作,决定从所随机抽取的市民中按年龄采用分层抽样的方法抽取20名接受采访,再从抽出的这20名中年龄在![]() 的选取2名担任主要发言人.记这2名主要发言人年龄在
的选取2名担任主要发言人.记这2名主要发言人年龄在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n是两条不同的直线,α、β是两个不同的平面,则下列命题不正确的是________.
(1).若m⊥n,m⊥α,n![]() α,则n∥α
α,则n∥α
(2).若m⊥β,α⊥β,则m∥α或m![]() α
α
(3).若m⊥n,m⊥α,n⊥β,则α⊥β
(4).若![]() ∥α,α⊥β,则
∥α,α⊥β,则![]() ⊥β
⊥β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,地面上有一竖直放置的圆形标志物,圆心为C,与地面的接触点为G.与圆形标志物在同一平面内的地面上点P处有一个观测点,且PG=50m.在观测点正前方10m处(即PD=10m)有一个高为10m(即ED=10m)的广告牌遮住了视线,因此在观测点所能看到的圆形标志的最大部分即为图中从A到F的圆弧. 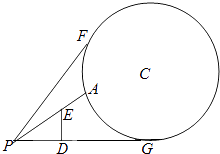
(1)若圆形标志物半径为25m,以PG所在直线为x轴,G为坐标原点,建立直角坐标系,求圆C和直线PF的方程;
(2)若在点P处观测该圆形标志的最大视角(即∠APF)的正切值为 ![]() ,求该圆形标志物的半径.
,求该圆形标志物的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com