Question

   

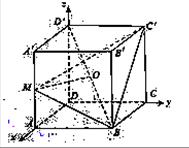
已知正方体ABCD－A'B'C'D'的棱长为1，点M是棱AA'的中点，点O是对角线BD'的中点.

（Ⅰ）求证：OM为异面直线AA'和BD'的公垂线；

（Ⅱ）求二面角M－BC'－B'的大小；

（Ⅲ）求三棱锥M－OBC的体积.    

 

 

 

 

Answer 1

【答案】

 

 

本小题主要考查异面直线、直线与平面垂直、二面角、正方体、三棱锥体积等基础知识，并考查空间想象能力和逻辑推理能力，考查应用向量知识解决数学问题的能力。

解法一：（1）连结AC，取AC中点K，则K为BD的中点，连结OK

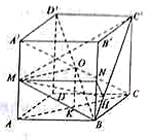因为M是棱AA’的中点，点O是BD’的中点

所以AM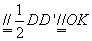

所以MO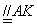  

由AA’⊥AK，得MO⊥AA’

因为AK⊥BD,AK⊥BB’，所以AK⊥平面BDD’B’

所以AK⊥BD’

所以MO⊥BD’

又因为OM是异面直线AA’和BD’都相交  

故OM为异面直线AA'和BD'的公垂线

（2）取BB’中点N，连结MN，则MN⊥平面BCC’B’

过点N作NH⊥BC’于H，连结MH

则由三垂线定理得BC’⊥MH

从而,∠MHN为二面角M-BC’-B’的平面角

MN=1,NH=Bnsin45°=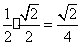

在Rt△MNH中，tan∠MHN=  

故二面角M-BC’-B’的大小为arctan2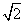

(3)易知，S_△OBC=S_△OA’D’，且△OBC和△OA’D’都在平面BCD’A’内

点O到平面MA’D’距离h＝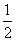

V_M-OBC=V_M-OA’D’=V_O-MA’D’=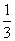S_△MA’D’h=

解法二：

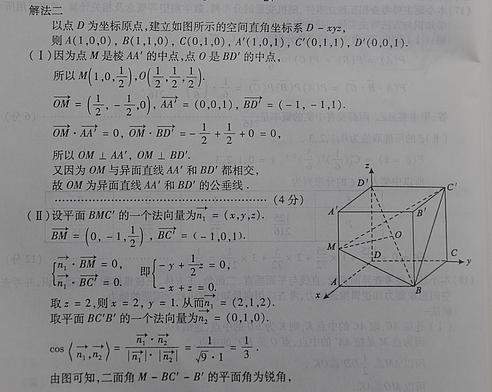
以点D为坐标原点，建立如图所示空间直角坐标系D-xyz

则A(1,0,0),B(1,1,0),C(0,1,0),A’(1,0,1),C’(0,1,1),D’(0,0,1)

(1)因为点M是棱AA’的中点,点O是BD’的中点

所以M(1,0, 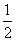),O(,,)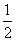

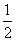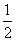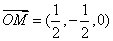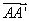,=(0,0,1),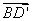=(-1,-1,1)

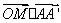=0, +0=0  

所以OM⊥AA’,OM⊥BD’

又因为OM与异面直线AA’和BD’都相交

故OM为异面直线AA'和BD'的公垂线.………………………………4分

(2)设平面BMC'的一个法向量为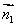=(x,y,z)

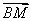=(0,-1,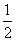), 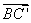＝(－1,0,1)

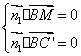  即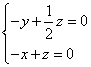

取z＝2,则x＝2,y＝1，从而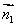=(2,1,2)    

取平面BC'B'的一个法向量为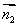＝(0,1,0)

cos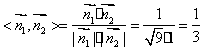

由图可知，二面角M-BC'-B'的平面角为锐角

故二面角M-BC'-B'的大小为arccos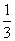………………………………………………9分

(3)易知，S_△OBC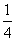＝S_△BCD'A'＝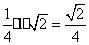

设平面OBC的一个法向量为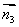＝(x₁,y₁,z₁)    

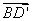＝(－1,－1,1), ＝(－1,0,0)

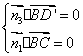  即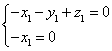

取z₁＝1,得y₁＝1，从而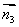＝(0,1,1)

点M到平面OBC的距离d＝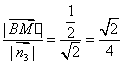  

V_M－OBC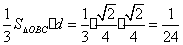＝…………………………………………12分