
分析 利用向量垂直与数量积的关系、向量共线定理、向量坐标运算性质即可得出.
解答 解:∵$\overrightarrow a⊥\overrightarrow c$,$\overrightarrow b∥\overrightarrow c$,
∴$\overrightarrow{a}•\overrightarrow{c}$=3x-6=0,3y+6=0,
解得x=2,y=-2,
∴$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(1,-2).
则$({\overrightarrow a+\overrightarrow b})•\overrightarrow c$=9+6=15.
故答案为:15.
点评 本题考查了向量垂直与数量积的关系、向量共线定理、向量坐标运算性质,考查了推理能力与计算能力,属于基础题.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
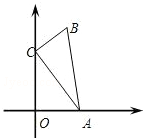 如图,在△ABC中,∠ACB=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离是1+$\sqrt{2}$.
如图,在△ABC中,∠ACB=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离是1+$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 4 | C. | 5 | D. | -3或4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.2 | B. | 0.4 | C. | 0.6 | D. | 0.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com