
分析 (1)根据题意,要求取出的4件产品没有一等品,即在3件二等品、2件三等品中任取4件,由组合数公式计算可得答案;
(2)根据题意,分3种情况讨论:①、取出的4件产品中有2件一等品、1件二等品、1件三等品,②、取出的4件产品中有1件一等品、2件二等品、1件三等品,③、取出的4件产品中有1件一等品、1件二等品、2件三等品,分别求出每一种情况的取法数目,由分类计数原理计算可得答案.
解答 解:(1)根据题意,有8件产品,其中一等品3件,二等品3件,三等品2件,
没有一等品,即在3件二等品、2件三等品中任取4件即可,
有C54=5种取法,
则没有一等品的不同抽法有5种,
(2)根据题意,分3种情况讨论:
①、取出的4件产品中有2件一等品、1件二等品、1件三等品,有C32C31C21=18种取法;
②、取出的4件产品中有1件一等品、2件二等品、1件三等品,有C31C32C21=18种取法;
③、取出的4件产品中有1件一等品、1件二等品、2件三等品,有C31C31C22=9种取法;
则不同的取法有18+18+9=45种;
故一等品,二等品,三等品至少一件的不同抽法有45种.
点评 本题考查排列、组合的实际应用,(2)注意要分情况讨论,要不重不漏.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源: 题型:选择题
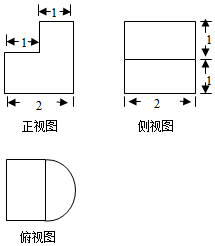
| A. | $\frac{1}{2}+\frac{π}{2}$ | B. | $1+\frac{π}{2}$ | C. | 1+π | D. | 2+π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com