
分析 (Ⅰ)求出函数f(x)的分段函数的形式,得到关于x的不等式组,解出即可;
(Ⅱ)由f(x)=1,求出交点的横坐标,求出三角形的底,根据三角形的面积求出a的值即可.
解答 解:(Ⅰ)由条件f(x)=$\left\{\begin{array}{l}{(1-a)x+a+1,x<-1}\\{-(a+1)x+a-1,-1≤x≤1}\\{(a-1)x-a-1,x>1}\end{array}\right.$,
a=2时,f(x)≥3?$\left\{\begin{array}{l}{x<-1}\\{-x+3≥3}\end{array}\right.$或$\left\{\begin{array}{l}{-1≤x≤1}\\{-3x+1≥3}\end{array}\right.$或$\left\{\begin{array}{l}{x>1}\\{x-3≥3}\end{array}\right.$
?x<-1或-1≤x≤-$\frac{2}{3}$或x≥6,
故不等式f(x)≥3的解集是(-∞,-$\frac{2}{3}$]∪[6,+∞);
(Ⅱ)由(Ⅰ)知,f(x)=1⇒x1=$\frac{a-2}{a+1}$,x2=$\frac{a+2}{a-1}$,
三角形的面积S=$\frac{1}{2}$•($\frac{a+2}{a-1}$-$\frac{a-2}{a+1}$)•3=$\frac{9a}{{a}^{2}-1}$=$\frac{27}{8}$,
解得:a=3或a=-$\frac{1}{3}$,
∵a>1
∴a=-$\frac{1}{3}$不符合题意
∴a=3
故所求a的值是3.
点评 本题考查了解绝对值不等式问题,考查分类讨论思想以及转化思想,是一道中档题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
| 身高x(cm) | 60 | 70 | 80 | 90 | 100 | 110 |
| 体重y(kg) | 6 | 8 | 10 | 14 | 15 | 18 |
| ${\widehate^{(1)}}$ | 0.41 | 0.01 | 1.21 | -0.19 | 0.41 | |
| ${\widehate^{(2)}}$ | -0.36 | 0.07 | 0.12 | 1.69 | -0.34 | -1.12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $a>2\sqrt{2}$ | B. | $2\sqrt{2}<a<3$ | C. | a>3 | D. | $3<a<2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{2}$i | C. | $±\frac{1}{2}$ | D. | $±\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{a}$ | B. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥($\overrightarrow{a}$+$\overrightarrow{b}$) | C. | ($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{b}$ | D. | ($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
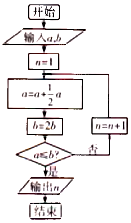 《算学启蒙》值中国元代数学家朱世杰撰写的一部数学启蒙读物,包括面积、体积、比例、开方、高次方程等问题,《算学启蒙》中有关于“松竹并生”的问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等”,如图是源于其思想的一个程序框图,若输入a,b分别为8,2,则输出的n等于( )
《算学启蒙》值中国元代数学家朱世杰撰写的一部数学启蒙读物,包括面积、体积、比例、开方、高次方程等问题,《算学启蒙》中有关于“松竹并生”的问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等”,如图是源于其思想的一个程序框图,若输入a,b分别为8,2,则输出的n等于( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
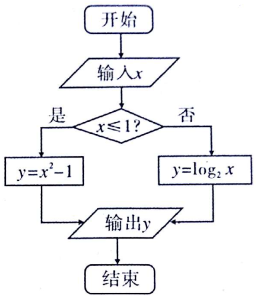 已知如图所示的程序框图的输入值x∈[-1,4],则输出y值的取值范围是( )
已知如图所示的程序框图的输入值x∈[-1,4],则输出y值的取值范围是( )| A. | [0,2] | B. | [-1,2] | C. | [-1,15] | D. | [2,15] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com