练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．求和5+55+555+…+$\underset{\underbrace{555…5}}{n个5}$=$\frac{5（{10}^{n}-1）}{81}-\frac{5}{9}n$．

    分析 由an=$\underset{\underset{555…5}{?}}{n个5}$=$\frac{5}{9}×$$\underset{\underset{999…9}{?}}{n个5}$=$\frac{5}{9}$（10n-1）．利用等比数列的前n项和公式即可得出．

    解答 解：∵an=$\underset{\underset{555…5}{?}}{n个5}$=$\frac{5}{9}×$$\underset{\underset{999…9}{?}}{n个5}$=$\frac{5}{9}$（10n-1）．
    ∴Sn=$\frac{5}{9}$（10+102+…+10n-n）
    =$\frac{5}{9}$[$\frac{10（{10}^{n}-1）}{10-1}$-n]
    =$\frac{5（{10}^{n}-1）}{81}-\frac{5}{9}n$．
    故答案为：$\frac{5（{10}^{n}-1）}{81}-\frac{5}{9}n$．

    点评 本题考查了等比数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届河南商丘第一高级中学年高三上理开学摸底数学试卷（解析版） 题型：选择题

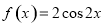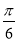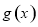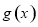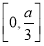    将函数的图象向右平移个单位后得到函数的图象．若函数在区间和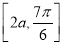上均单调递增，则实数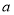的取值范围是（ ）

    A． B．

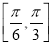    C． D．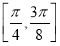

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知三棱锥V-ABC的顶点都在球O的球面上，AB=3，AC=4，AB⊥AC，VA=VB=VC=5，则球O的半径为$\frac{5\sqrt{3}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

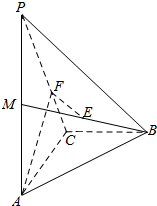    6．如图，在四面体P-ABC中，PA⊥面ACB，BC⊥AC，M是PA的中点，E是BM的中点，AC=2，PA=4，F是线段PC上的点，且EF∥面ACB．
    （Ⅰ）求证：BC⊥AF
    （Ⅱ）求$\frac{CF}{CP}$；
    （Ⅲ）若异面直线EF与CA所成角为45°，求EF与面PAB所成角θ的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．高考复习经过二轮“见多识广”之后，为了研究考前“限时抢分”强化训练次数x与答题正确率y%的关系，对某校高三某班学生进行了关注统计，得到如下数据：
    x1234
    y20305060
    （Ⅰ）求y关于x的线性回归方程，并预测答题正确率是100%的强化训练次数；
    （Ⅱ）若用$\frac{y_i}{{{x_i}+3}}$（i=1，2，3，4）表示统计数据的“强化均值”（精确到整数），若“强化均值”的标准差在区间[0，2）内，则强化训练有效，请问这个班的强化训练是否有效？
    附：回归直线的斜率和截距的最小二乘法估计公式分别为：$\hat b=\frac{{\sum_{i=1}^n{（{x_i}-\bar x）（{y_i}-\bar y）}}}{{\sum_{i=1}^n{{{（{x_i}-\bar x）}^2}}}}$，$\hat a=\bar y-\hat b\bar x$．
    样本数据x1，x2，…，xn的标准差为：s=$\sqrt{\frac{{\sum_{i=1}^n{{{（{x_i}-\bar x）}^2}}}}{n}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$，右顶点为（2，0），离心率为$\frac{{\sqrt{3}}}{2}$，直线l1：y=kx+m（k≠0，m≠0）与椭圆C相交于不同的两点A，B，过AB的中点M作垂直于l1的直线l2，设l2与椭圆C相交于不同的两点C，D，且CD的中点为N．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）设原点O到直线l1的距离为d，求$\frac{{|{MN}|}}{d}$的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知f（$\frac{1}{x}$）=$\frac{x}{1+x}$，则f′（x）=$\frac{1}{（x+1）^{2}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个观测点C与D，测得∠BCD=15°，∠BDC=30°，CD=30米，并在C测得塔顶A的仰角为60°，则塔的高度AB为（　　）
    A．15$\sqrt{2}$米B．15$\sqrt{3}$米C．15（$\sqrt{3}$+1）米D．15$\sqrt{6}$米

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

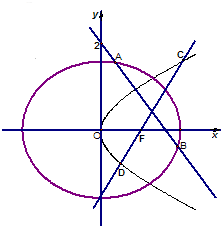    8．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为$\frac{1}{2}$，椭圆C的右焦点F和抛物线G：y2=4x的焦点相同．
    （1）求椭圆C的方程．
    （2）如图，已知直线l：y=kx+2与椭圆C及抛物线G都有两个不同的公共点，且直线l与椭圆C交于A，B两点；过焦点F的直线l′与抛物线G交于C，D两点，记$λ=\overrightarrow{OA}•\overrightarrow{OB}-\overrightarrow{OC}•\overrightarrow{OD}$，求λ的取值范围．

    查看答案和解析>>

    同步练习册答案