
分析 (1)根据条件,由2∈A便可得出$\frac{1}{1-2}∈A$,进而$\frac{1}{1-\frac{1}{1-2}}∈A$,从而可以求出集合A的另外的两个元素;
(2)根据条件,a∈A得出$\frac{1}{1-a}∈A$,同样得出$\frac{1}{1-\frac{1}{1-a}}∈A$,化简后即可得出结论成立;
(3)可考虑反证法,假设A为单元素集,从而得出a=$\frac{1}{1-a}$,只需说明该方程无解即可.
解答 解:(1)根据条件,若2∈A,则$\frac{1}{1-2}=-1∈A$,$\frac{1}{1-(-1)}=\frac{1}{2}∈A$;
∴这两个元素为$-1,\frac{1}{2}$;
(2)证明:若a∈A,a≠1,则$\frac{1}{1-a}∈A$;
∴$\frac{1}{1-\frac{1}{1-a}}=1-\frac{1}{a}∈A$;
(3)证明:若A为单元素集,则a=$\frac{1}{1-a}$;
整理成,a2-a+1=0;
△=1-4<0;
∴该方程无解;
即A不可能是单元素集.
点评 考查元素与集合的关系,理解集合A所满足的条件,反证法证明问题的方法和过程,以及单元素集的定义,一元二次方程实根的判断.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$] | B. | (-∞,-$\frac{\sqrt{2}}{2}$]∪[$\frac{\sqrt{2}}{2}$,+∞) | C. | [-$\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{2}}{2}$]∪[$\frac{\sqrt{2}}{2}$,$\frac{2\sqrt{5}}{5}$] | D. | (-$\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{2}}{2}$]∪[$\frac{\sqrt{2}}{2}$,$\frac{2\sqrt{5}}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
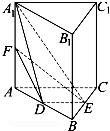 在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=1,AA1=2,D、E分别为棱AB、BC的中点,点F在棱AA1上.
在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=1,AA1=2,D、E分别为棱AB、BC的中点,点F在棱AA1上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3+4i | B. | $\frac{3}{5}$+$\frac{4}{5}$i | C. | $\frac{3}{15}$-$\frac{4}{15}$i | D. | $\frac{3}{25}$-$\frac{4}{25}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=ex+e-x | B. | f(x)=ex-e-x | C. | f(x)=x|x| | D. | f(x)=cos(x-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com