
 ) .已知函数y=
) .已知函数y= f(x)=
f(x)=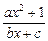 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<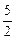
 明理由.
明理由. 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:单选题
| A.存在a∈R,f(x)是偶函数 |
| B.存在a∈R,f(x)是奇函数 |
| C.对于任意的a∈R,f(x)在(0,+∞)上是增函数 |
| D.对于任意的a∈R,f(x)在(0,+∞)上是减函数 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg,针对这种销售情况,
为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg,针对这种销售情况, 为y元,求y与x的函数关系式;
为y元,求y与x的函数关系式;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
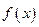 的定义域为
的定义域为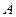 ,若
,若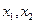
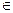
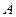 ,且
,且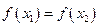
 时总有
时总有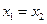 ,则称
,则称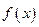 为单一函数.如
为单一函数.如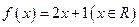 是单一函数,下列命题正确的是____▲____.(写出所有正确答案)
是单一函数,下列命题正确的是____▲____.(写出所有正确答案)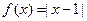
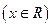 是单一函数;
是单一函数;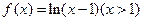 是单一函数;
是单一函数; 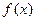 为单一函数,
为单一函数,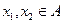 且
且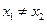 ,则
,则
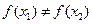 ;
; 定是单调函数.
定是单调函数. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com