
| A. | $3\sqrt{2}$ | B. | $\frac{9}{2}$ | C. | 9 | D. | $\frac{{3\sqrt{2}}}{2}$ |
分析 方法一:由x,y∈R+,则满足$\left\{\begin{array}{l}{x+1≥0}\\{y+\sqrt{3}≥0}\end{array}\right.$,根据柯西不等式可得$\sqrt{x+1}+\sqrt{y+3}$≤$\sqrt{2}$•$\sqrt{x+1+y+3}$=$\sqrt{2}$•$\sqrt{9}$=3$\sqrt{2}$,当且仅当$\sqrt{x+1}$=$\sqrt{y+3}$,即x=$\frac{7}{2}$,y=$\frac{3}{2}$时等号成立,即可求得$\sqrt{x+1}+\sqrt{y+3}$的最大值;
方法二:x,y∈R+,且x+y=5,y+3=8-x,Z=$\sqrt{x+1}+\sqrt{y+3}$=$\sqrt{x+1}$+$\sqrt{8-x}$,($\sqrt{x+1}$)2+($\sqrt{8-x}$)2=9,设$\sqrt{x+1}$=3sinα,$\sqrt{8-x}$=3cosα,(0≤α≤$\frac{π}{2}$),根据辅助角公式及正弦函数图象及最值,即可求得$\sqrt{x+1}+\sqrt{y+3}$的最大值.
解答 解:方法一:x,y∈R+,则满足$\left\{\begin{array}{l}{x+1≥0}\\{y+\sqrt{3}≥0}\end{array}\right.$,
根据柯西不等式可得$\sqrt{x+1}+\sqrt{y+3}$≤$\sqrt{2}$•$\sqrt{x+1+y+3}$=$\sqrt{2}$•$\sqrt{9}$=3$\sqrt{2}$,
当且仅当$\sqrt{x+1}$=$\sqrt{y+3}$,即x=$\frac{7}{2}$,y=$\frac{3}{2}$时等号成立.
∴则$\sqrt{x+1}+\sqrt{y+3}$的最大值3$\sqrt{2}$,
故选A.
方法二:x,y∈R+,且x+y=5,
故y=5-x,
y+3=8-x,
则Z=$\sqrt{x+1}+\sqrt{y+3}$=$\sqrt{x+1}$+$\sqrt{8-x}$,
∵($\sqrt{x+1}$)2+($\sqrt{8-x}$)2=x+1+8-x=9,
∴设$\sqrt{x+1}$=3sinα,$\sqrt{8-x}$=3cosα,(0≤α≤$\frac{π}{2}$),
则Z=$\sqrt{x+1}+\sqrt{y+3}$=$\sqrt{x+1}$+$\sqrt{8-x}$=3sinα+3cosα=3$\sqrt{2}$sin(α+$\frac{π}{4}$),
故当α+$\frac{π}{4}$=$\frac{π}{2}$,即α=$\frac{π}{4}$时,Z取最大值3$\sqrt{2}$,
则$\sqrt{x+1}+\sqrt{y+3}$的最大值3$\sqrt{2}$,
故选A.
点评 本题考查柯西不等式的应用,考查正弦函数的图象及性质,考查辅助角公式的应用,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $y=\sqrt{x}$与y2=x | B. | y=x与$\frac{x}{y}=1$ | C. | y2-x2=0与|y|=|x| | D. | y=x0与y=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
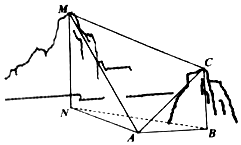 如图,为测量山高l,选择A和另一座山的山顶|PA|为测量观测点.从MB=MC点测得△ABC点的仰角60°,C点的仰角45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=150m.
如图,为测量山高l,选择A和另一座山的山顶|PA|为测量观测点.从MB=MC点测得△ABC点的仰角60°,C点的仰角45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=150m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{3}π$ | B. | $\frac{1}{3}π$ | C. | $\frac{2}{3}π$ | D. | $\frac{{2\sqrt{2}}}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4f(1)<f(2) | B. | 4f(1)>f(2) | C. | f(1)<4f(2) | D. | f(1)<2f'(2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
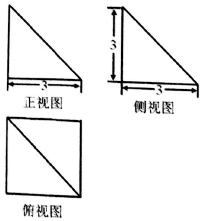
| A. | $\frac{27}{2}π$ | B. | 27π | C. | 27$\sqrt{3}$π | D. | $\frac{27\sqrt{3}π}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com