
【题目】有六名同学参加演讲比赛,编号分别为1,2,3,4,5,6,比赛结果设特等奖一名,![]() ,
,![]() ,
,![]() ,
,![]() 四名同学对于谁获得特等奖进行预测.
四名同学对于谁获得特等奖进行预测.![]() 说:不是1号就是2号获得特等奖;
说:不是1号就是2号获得特等奖;![]() 说:3号不可能获得特等奖;
说:3号不可能获得特等奖;![]() 说:4,5,6号不可能获得特等奖;
说:4,5,6号不可能获得特等奖;![]() 说:能获得特等奖的是4,5,6号中的一个.公布的比赛结果表明,
说:能获得特等奖的是4,5,6号中的一个.公布的比赛结果表明,![]() ,
,![]() ,
,![]() ,
,![]() 中只有一个判断正确.根据以上信息,获得特等奖的是( )号同学.
中只有一个判断正确.根据以上信息,获得特等奖的是( )号同学.
A.1B.2C.3D.4,5,6号中的一个
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
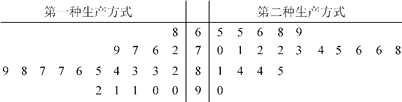
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知圆方程为![]() ,过圆上任意一点作圆的切线,切线与椭圆
,过圆上任意一点作圆的切线,切线与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,设
为坐标原点,设![]() 为
为![]() 的中点,求
的中点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 是由两个定点
是由两个定点![]() 和点
和点![]() 的距离之积等于
的距离之积等于![]() 的所有点组成的,对于曲线
的所有点组成的,对于曲线![]() ,有下列四个结论:①曲线
,有下列四个结论:①曲线![]() 是轴对称图形;②曲线
是轴对称图形;②曲线![]() 上所有的点都在单位圆
上所有的点都在单位圆![]() 内;③曲线
内;③曲线![]() 是中心对称图形;④曲线
是中心对称图形;④曲线![]() 上所有点的纵坐标
上所有点的纵坐标![]() .其中,所有正确结论的序号是______.
.其中,所有正确结论的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,已知![]() 是以
是以![]() 的直角三角形铁皮,
的直角三角形铁皮,![]() 米,
米,![]() 分别是边
分别是边![]() 上不与端点重合的动点,且
上不与端点重合的动点,且![]() .现将
.现将![]() 铁皮沿
铁皮沿![]() 折起至
折起至![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,连接
,连接![]() ,如图所示.现要制作一个四棱锥
,如图所示.现要制作一个四棱锥![]() 的封闭容器,其中
的封闭容器,其中![]() 铁皮和直角梯形
铁皮和直角梯形![]() 铁皮分别是这个封闭容器的一个侧面和底面,其他三个侧面用相同材料的铁皮无缝焊接密封而成(假设制作过程中不浪费材料,且铁皮厚度忽略不计).
铁皮分别是这个封闭容器的一个侧面和底面,其他三个侧面用相同材料的铁皮无缝焊接密封而成(假设制作过程中不浪费材料,且铁皮厚度忽略不计).
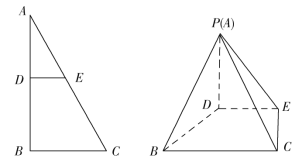
(1)若![]() 为
为![]() 边的中点,求制作三个新增侧面的铁皮面积是多少平方米?
边的中点,求制作三个新增侧面的铁皮面积是多少平方米?
(2)求这个封闭容器的最大体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x),g(x)分别是定义在R上的奇函数和偶函数,f′(x),g'(x)为其导函数,当x<0时,f′(x)![]() g(x)+f(x)
g(x)+f(x)![]() g'(x)<0且g(﹣3)=0,则使得不等式f(x)
g'(x)<0且g(﹣3)=0,则使得不等式f(x)![]() g(x)<0成立的x的取值范围是( )
g(x)<0成立的x的取值范围是( )
A.(﹣∞,﹣3)B.(﹣3,0)C.(0,3)D.(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是边长
是边长![]() ,
,![]() 的矩形硬纸片,在硬纸片的四角切去边长相等的小正方形后,再沿虚线折起,做成一个无盖的长方体盒子,
的矩形硬纸片,在硬纸片的四角切去边长相等的小正方形后,再沿虚线折起,做成一个无盖的长方体盒子,![]() 、
、![]() 是
是![]() 上被切去的小正方形的两个顶点,设
上被切去的小正方形的两个顶点,设![]() .
.

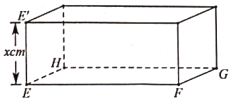
(1)将长方体盒子体积![]() 表示成
表示成![]() 的函数关系式,并求其定义域;
的函数关系式,并求其定义域;
(2)当![]() 为何值时,此长方体盒子体积
为何值时,此长方体盒子体积![]() 最大?并求出最大体积.
最大?并求出最大体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com