Question

4．已知函数f（x）=x•e^x+e^-x，x∈R．
（Ⅰ）求函数y=f（x）•e^x的单调区间；
（Ⅱ）若对于任意的x＞0，总有f（x）≥ax²+1，求实数a的取值范围；
（Ⅲ）证明：对于任意的x₁，x₂，h其中x₁＜x₂，h＞0，总有f（x₁）+f（x₂）＜f（x₁-h）+f（x₂+h）．

Answer 1

分析 （1）求导数，分析导数符号即得；（2）构造函数是解题关键．构造新的函数多重求导，判断函数单调性，可得；（3）利用数形结合的思想可解．

解答 解：（1）y=f（x）•e^x=x•e^2x+1，
∴f′（x）=e^2x+2x•e^2x=e^2x（1+2x），
令f′（x）＞0得：$x＞-\frac{1}{2}$，
令f′（x）＜0得：$x＜-\frac{1}{2}$，
故函数的单调增区间为$（-\frac{1}{2}，+∞）$，减区间为$（-∞，-\frac{1}{2}）$；
（2）设g（x）=f（x）-ax²-1=x•e^x+e^-x-ax²-1，（x＞0）
则g′（x）=e^x（x+1）-e^-x-2ax，
设h（x）=g′（x），
则h′（x）=e^x（x+2）+e^-x-2a，
再设l（x）=h′（x），
则l′（x）=e^x（x+3）-e^-x，
易知l′（x）为增函数，故有l′（x）＞l′（0）=2＞0，
∴l（x）＞l（0）=3-2a，
①当$a≤\frac{3}{2}$时，l（x）＞0，即h′（x）=e^x（x+2）+e^-x-2a＞0，
所以g′（x）=e^x（x+1）-e^-x-2ax为增函数，故有g′（x）＞g′（0）=0，
∴此时g（x）为增函数，所以g（x）＞g（0）=0，满足题意；
②当$a＞\frac{3}{2}$时，l（0）＜0，
∵l（lna）=$alna+\frac{1}{a}＞0$，
∴存在x₀∈（0，lna），l（x₀）=0，
∴当x₀∈（0，x₀）时，h′（x）＜0，
∴h（x）＜h（0）=0，
∴此时g′（x）＜0，
∴g（x）＜g（0）=0，不合题意．
综上所述，a的范围是$（-∞，\frac{3}{2}]$．
（3）设m（x）=f′（x）=（x+1）e^x-e^-x，
显然，当x≥0时，f′（x）≥0；
当x≤-1时，f′（x）＜0，
 当-1＜x＜0时，0＜x+1＜1，${\frac{1}{e}＜e}^{x}＜1$，e^-x＞1，
∴f′（x）＜0，
故当x＜0时，有f′（x）＜0，
m′（x）=（x+2）e^x+e^-x，易知m′（x）＞0，故函数f（x）在R上的图象大致为：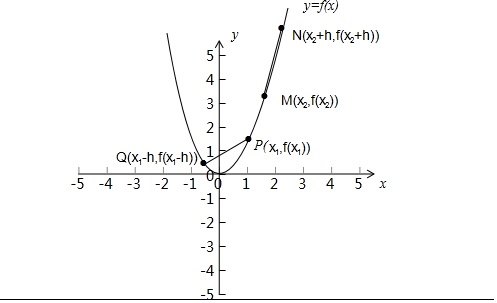

图象在y轴左侧递减且速度越来越慢，在y轴右侧递增，且速度越来越快，由图可知：k_PQ＜k_MN，
即$\frac{f（{x}_{1}-h）-f（{x}_{1}）}{-h}$＜$\frac{f（{x}_{2}+h）-f（{x}_{2}）}{h}$，
变形得f（x₁）+f（x₂）＜f（x₁-h）+f（x₂+h）
同理当x₁＜0时也可得结果．
综上所述有：f（x₁）+f（x₂）＜f（x₁-h）+f（x₂+h）．

点评 本题考查导数的应用．正确掌握导数与函数单调性的关系是解题关键．属于难题．