
设直线 与抛物线
与抛物线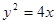 交于
交于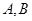 两点.
两点.
(1)求线段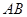 的长;(2)若抛物线
的长;(2)若抛物线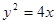 的焦点为
的焦点为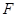 ,求
,求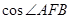 的值.
的值.
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 8 |
| 3 |
| 1 |
| 4 |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年长沙一中第八次月考理)(13分)已知直线L:x-y-3=0,抛物线C的顶点在原点,焦点在![]() 轴正半轴上,S是抛物线C上任意一点,T是直线L上任意一点,若|ST|的最小值为d>0时,点S的横坐标为2.
轴正半轴上,S是抛物线C上任意一点,T是直线L上任意一点,若|ST|的最小值为d>0时,点S的横坐标为2.
(1)求抛物线方程以及d的值;
(2)过抛物线C的对称轴上任一点![]() 作直线与抛物线交于
作直线与抛物线交于![]() 两点,点
两点,点![]() 是点
是点![]() 关于原点的对称点.设点
关于原点的对称点.设点![]() 分有向线段
分有向线段![]() 所成的比为
所成的比为![]() ,
,
证明:![]() ;
;
查看答案和解析>>
科目:高中数学 来源:2014届浙江效实中学高二上期末考试理科数学试卷(解析版) 题型:解答题
已知抛物线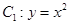 ,
,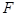 为抛物线的焦点,椭圆
为抛物线的焦点,椭圆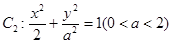 ;
;
(1)若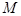 是
是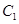 与
与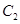 在第一象限的交点,且
在第一象限的交点,且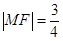 ,求实数
,求实数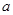 的值;
的值;
(2)设直线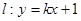 与抛物线
与抛物线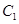 交于
交于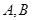 两个不同的点,
两个不同的点,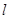 与椭圆
与椭圆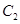 交于
交于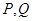 两个
两个
不同点,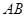 中点为
中点为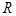 ,
,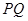 中点为
中点为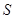 ,若
,若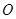 在以
在以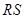 为直径的圆上,且
为直径的圆上,且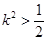 ,求实数
,求实数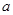
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届广东汕头金山中学高二上期末考试理科数学试卷(解析版) 题型:解答题
(本小题满分14分)设椭圆 与抛物线
与抛物线 的焦点均在
的焦点均在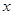 轴上,
轴上, 的中心和
的中心和 的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1)求 ,
, 的标准方程, 并分别求出它们的离心率
的标准方程, 并分别求出它们的离心率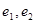 ;
;
2)设直线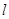 与椭圆
与椭圆 交于不同的两点
交于不同的两点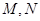 ,且
,且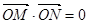 (其中
(其中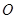 坐标原点),请问是否存在这样的直线
坐标原点),请问是否存在这样的直线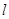 过抛物线
过抛物线 的焦点
的焦点 若存在,求出直线
若存在,求出直线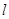 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2012届黑龙江省下学期高二期末考试数学试题(文科) 题型:解答题
设抛物线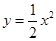 的焦点为F,准线为
的焦点为F,准线为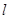 ,过点F作一直线与抛物线交于A、B两点,再分别过点A、B作抛物线的切线,这两条切线的交点记为P.
,过点F作一直线与抛物线交于A、B两点,再分别过点A、B作抛物线的切线,这两条切线的交点记为P.
(1)证明:直线PA与PB相互垂直,且点P在准线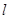 上;
上;
(2)是否存在常数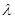 ,使等式
,使等式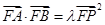 恒成立?若存在,求出
恒成立?若存在,求出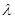 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com