
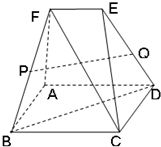
 如图,多面体ABCDEF中,四边形ABCD是边长为2a的正方形,BD⊥CF,且FA⊥AD,EF∥AD,EF=AF=a.
如图,多面体ABCDEF中,四边形ABCD是边长为2a的正方形,BD⊥CF,且FA⊥AD,EF∥AD,EF=AF=a.分析 (Ⅰ)连结AC,推导出BD⊥AC,从而FA⊥平面ADEF,由此能证明平面ADEF垂直于平面ABCD.
(Ⅱ)作PS⊥AB,QT⊥AD,EM⊥AD,S,T,M是垂足,推导出四边形PSTQ是平行四边形,从而PQ∥ST,由此能证明PQ∥平面ABCD.
(Ⅲ)多面体ABCDEF的体积V多面体ABCDEF=VF-ABCD+VC-DEF,由此能求出结果.
解答 证明:(Ⅰ)连结AC,∵ABCD是正方形,∴BD⊥AC,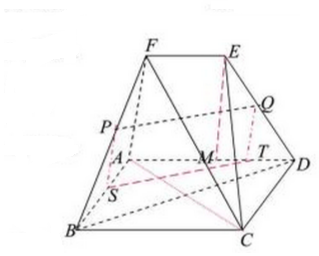
∵平面ABCD⊥平面ADEF,AF⊥AD,平面ABCD∩平面ADEF=AD,
∴FA⊥平面ADEF,
∴平面ADEF垂直于平面ABCD.
(Ⅱ)作PS⊥AB,QT⊥AD,EM⊥AD,S,T,M是垂足,
在△ABF中,PS:AF=BP:BF=1:2,PS=$\frac{1}{2}$AF,
在直角梯形ADEF中,QT=$\frac{1}{2}$EM=$\frac{1}{2}$AF,
∴PS$\underset{∥}{=}$QT,
∴四边形PSTQ是平行四边形,∴PQ∥ST,
∵ST?平面ABCD,∴PQ∥平面ABCD.
解:(Ⅲ)多面体ABCDEF的体积:
V多面体ABCDEF=VF-ABCD+VC-DEF
=$\frac{1}{3}×(2a)^{2}×a+\frac{1}{3}×\frac{1}{2}×{a}^{2}×2a$=$\frac{5}{3}{a}^{3}$.
点评 本题考查面面垂直、线面平行的证明,考查多面体的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 11 | C. | 10 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${e}^{{x}_{1}}$f(x2)>${e}^{{x}_{2}}$ex2f(x1) | |
| B. | ${e}^{{x}_{1}}$f(x2)<${e}^{{x}_{2}}$f(x1) | |
| C. | ${e}^{{x}_{1}}$f(x2)=${e}^{{x}_{2}}$f(x1) | |
| D. | ${e}^{{x}_{1}}$f(x2)与${e}^{{x}_{2}}$f(x1)的大小关系不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com