
分析 (Ⅰ)设中心所在直线为x+3y+c=0,结合正方形的性质和平行线间的距离公式求得c的值;
(Ⅱ)由平行线间的距离公式得正方形的边长.设正方形BC,AD所方程为3x-y+m=0,联立点G所在直线x0+3y0+1=0,得到$\left\{\begin{array}{l}x=\frac{-3m+5}{10}\\ y=\frac{m+15}{10}\end{array}$.结合限制性条件正方形仅有两个顶点在第一象限,得到-15<m<$\frac{5}{3}$,易求x0的取值范围为$(\frac{6}{5},\frac{13}{5})$.
解答 解:(Ⅰ)由于正方形中心G所在直线平行于直线x+3y-5=0,
设中心所在直线为x+3y+c=0,
由平行线间的距离公式得$\frac{|c+5|}{\sqrt{{1}^{2}+{3}^{2}}}$=$\frac{|c-7|}{\sqrt{{1}^{2}+{3}^{2}}}$.
解得c=1.
则正方形中心G所在的直线方程为x+3y+1=0;
(Ⅱ)由平行线间的距离公式得正方形的边长为d=$\frac{|7+5|}{\sqrt{{1}^{2}+{3}^{2}}}$=$\frac{12}{\sqrt{10}}$.
设正方形BC,AD所在直线方程为3x-y+m=0,
由于中心G(x0,y0)到BC的距离等于$\frac{d}{2}$=$\frac{6}{\sqrt{10}}$,
那么$\frac{|3{x}_{0}-{y}_{0}+m|}{\sqrt{{1}^{2}+{3}^{2}}}$=$\frac{6}{\sqrt{10}}$,
解得m=±6-3x0+y0 ①,
又因为G在直线x+3y+1=0上,那么x0+3y0+1=0,即y0=-$\frac{{x}_{0}+1}{3}$②,
把②代入①得m=±6-$\frac{10{x}_{0}+1}{3}$③,
联立方程$\left\{\begin{array}{l}x+3y-5=0\\ 3x-y+m=0\end{array}$,
解得$\left\{\begin{array}{l}x=\frac{-3m+5}{10}\\ y=\frac{m+15}{10}\end{array}$.
由于正方形只有两个点在第一象限,那么$\left\{\begin{array}{l}x>0\\ y>0\end{array}$,
就是$\left\{\begin{array}{l}\frac{-3m+5}{10}>0\\ \frac{m+15}{10}>0\end{array}$,
解得-15<m<$\frac{5}{3}$⑤,
把③代入⑤得到-15<±6-$\frac{10{x}_{0}+1}{3}$<$\frac{5}{3}$,
解得$\frac{6}{5}$<x0<$\frac{13}{5}$.
故x0的取值范围为$(\frac{6}{5},\frac{13}{5})$.
点评 本题考查两平行直线的距离公式的运用,待定系数法求直线方程以及正方形的性质,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
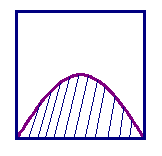 如图所示,墙上挂有一块边长为π的正方形木板,上面画有正弦曲线半个周期的图案(阴影部分).某人向此板投镖,假设每次都能击中木板并且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是( )
如图所示,墙上挂有一块边长为π的正方形木板,上面画有正弦曲线半个周期的图案(阴影部分).某人向此板投镖,假设每次都能击中木板并且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{π^2}$ | D. | $\frac{1}{2π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2) | B. | (2,3] | C. | (-∞,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{3}$ | B. | $\frac{13}{6}$ | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$≤t≤$\frac{1}{2}$ | B. | -2≤t≤2 | ||
| C. | t≥$\frac{1}{2}$或t≤-$\frac{1}{2}$或t=0 | D. | t≥2或t≤-2或t=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com