
| A. |  | B. |  | C. | 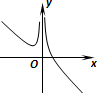 | D. |  |
分析 分三种情况讨论,根据函数的单调性和基本不等式即可判断.
解答 解:当a=0时,f(x)=|x|,且x≠0,故A符合,
当x>0时,且a>0时,f(x)=x+$\frac{a}{x}$≥2$\sqrt{a}$,当x<0时,且a>0时,f(x)=-x+$\frac{a}{x}$在(-∞,0)上为减函数,故B符合,
当x<0时,且a<0时,f(x)=-x+$\frac{a}{x}$≥2$\sqrt{-x•\frac{a}{x}}$=2$\sqrt{-a}$,当x>0时,且a<0时,f(x)=x+$\frac{a}{x}$在(0,+∞)上为增函数,故D符合,
故选:C.
点评 本题考查了函数图象的识别,关键是分类讨论,利用基本不等式和函数的单调性,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {0,1,2} | C. | (-1,3) | D. | {-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若直线l1∥平面α,直线l2∥平面α,则l1∥l2 | |
| B. | 若直线l上有两个点到平面α的距离相等,则l∥α | |
| C. | 直线l与平面α所成角的取值范围是(0,$\frac{π}{2}$) | |
| D. | 若直线l1⊥平面α,直线l2⊥平面α,则l1∥l2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,圆锥形容器的高为h,圆锥内水面的高为h1,且h${\;}_{1}=\frac{1}{3}h$,若将圆锥的倒置,水面高为h2,则h2等于( )
如图,圆锥形容器的高为h,圆锥内水面的高为h1,且h${\;}_{1}=\frac{1}{3}h$,若将圆锥的倒置,水面高为h2,则h2等于( )| A. | $\frac{2}{3}$h | B. | $\frac{19}{27}h$ | C. | $\frac{\root{3}{6}}{3}$h | D. | $\frac{\root{3}{19}}{3}$h |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 2$\sqrt{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com