
【题目】某企业质量检验员为了检测生产线上零件的质量情况,从生产线上随机抽取了![]() 个零件进行测量,根据所测量的零件尺寸(单位:mm),得到如下的频率分布直方图:
个零件进行测量,根据所测量的零件尺寸(单位:mm),得到如下的频率分布直方图:

(1)根据频率分布直方图,求这![]() 个零件尺寸的中位数(结果精确到
个零件尺寸的中位数(结果精确到![]() );
);
(2)若从这![]() 个零件中尺寸位于
个零件中尺寸位于![]() 之外的零件中随机抽取
之外的零件中随机抽取![]() 个,设
个,设![]() 表示尺寸在
表示尺寸在![]() 上的零件个数,求
上的零件个数,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(3)已知尺寸在![]() 上的零件为一等品,否则为二等品,将这
上的零件为一等品,否则为二等品,将这![]() 个零件尺寸的样本频率视为概率. 现对生产线上生产的零件进行成箱包装出售,每箱
个零件尺寸的样本频率视为概率. 现对生产线上生产的零件进行成箱包装出售,每箱![]() 个. 企业在交付买家之前需要决策是否对每箱的所有零件进行检验,已知每个零件的检验费用为
个. 企业在交付买家之前需要决策是否对每箱的所有零件进行检验,已知每个零件的检验费用为![]() 元. 若检验,则将检验出的二等品更换为一等品;若不检验,如果有二等品进入买家手中,企业要向买家对每个二等品支付
元. 若检验,则将检验出的二等品更换为一等品;若不检验,如果有二等品进入买家手中,企业要向买家对每个二等品支付![]() 元的赔偿费用. 现对一箱零件随机抽检了
元的赔偿费用. 现对一箱零件随机抽检了![]() 个,结果有
个,结果有![]() 个二等品,以整箱检验费用与赔偿费用之和的期望值作为决策依据,该企业是否对该箱余下的所有零件进行检验?请说明理由.
个二等品,以整箱检验费用与赔偿费用之和的期望值作为决策依据,该企业是否对该箱余下的所有零件进行检验?请说明理由.
【答案】(1)![]() ;(2)分布列见详解,期望为
;(2)分布列见详解,期望为![]() ;(3)余下所有零件不用检验,理由见详解.
;(3)余下所有零件不用检验,理由见详解.
【解析】
(1)计算![]() 的频率,并且与
的频率,并且与![]() 进行比较,判断中位数落在的区间,然后根据频率的计算方法,可得结果.
进行比较,判断中位数落在的区间,然后根据频率的计算方法,可得结果.
(2)计算位于![]() 之外的零件中随机抽取
之外的零件中随机抽取![]() 个的总数,写出
个的总数,写出![]() 所有可能取值,并计算相对应的概率,列出分布列,计算期望,可得结果.
所有可能取值,并计算相对应的概率,列出分布列,计算期望,可得结果.
(3)计算整箱的费用,根据余下零件个数服从二项分布,可得余下零件个数的期望值,然后计算整箱检验费用与赔偿费用之和的期望值,进行比较,可得结果.
(1)尺寸在![]() 的频率:
的频率:
![]()
尺寸在![]() 的频率:
的频率:![]()
且![]()
所以可知尺寸的中位数落在![]()
假设尺寸中位数为![]()
所以![]()
所以这![]() 个零件尺寸的中位数
个零件尺寸的中位数![]()
(2)尺寸在![]() 的个数为
的个数为![]()
尺寸在![]() 的个数为
的个数为![]()
![]() 的所有可能取值为1,2,3,4
的所有可能取值为1,2,3,4
则![]() ,
,![]()
![]() ,
,![]()
所以![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
![]()
(3)二等品的概率为![]()
如果对余下的零件进行检验则整箱的检验费用为
![]() (元)
(元)
余下二等品的个数期望值为![]()
如果不对余下的零件进行检验,
整箱检验费用与赔偿费用之和的期望值为
![]() (元)
(元)
所以![]() ,所以可以不对余下的零件进行检验.
,所以可以不对余下的零件进行检验.


 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:
【题目】已知一个放置在水平桌面上的密闭直三棱柱![]() 容器,如图1,
容器,如图1,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,里面装有体积为
,里面装有体积为![]() 的液体,现将该棱柱绕
的液体,现将该棱柱绕![]() 旋转至图2.在旋转过程中,以下命题中正确的个数是( )
旋转至图2.在旋转过程中,以下命题中正确的个数是( )

①液面刚好同时经过![]() ,
,![]() ,
,![]() 三点;
三点;
②当平面![]() 与液面成直二面角时,液面与水平桌面的距离为
与液面成直二面角时,液面与水平桌面的距离为![]() ;
;
③当液面与水平桌面的距离为![]() 时,
时,![]() 与液面所成角的正弦值为
与液面所成角的正弦值为![]() .
.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三数学奥林匹克竞赛集训队的一次数学测试成绩的茎叶图(图1)和频率分布直方图(图2)都受到不同程度的破坏,可见部分如图所示,据此解答如下问题.
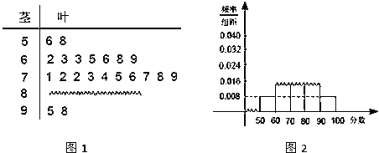
(1)求该集训队总人数及分数在[80,90)之间的频数;
(2)计算频率分布直方图中[80,90)的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生的答题情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】密云某商场举办春节优惠酬宾赠券活动,购买百元以上单件商品可以使用优惠劵一张,并且每天购物只能用一张优惠券.一名顾客得到三张优惠券,三张优惠券的具体优惠方式如下:
优惠券1:若标价超过50元,则付款时减免标价的10%;
优惠券2:若标价超过100元,则付款时减免20元;
优惠券3:若标价超过100元,则超过100元的部分减免18%.
如果顾客需要先用掉优惠券1,并且使用优惠券1比使用优惠券2、优惠券3减免的都多,那么你建议他购买的商品的标价可以是__________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人独立地对某一技术难题进行攻关.甲能攻克的概率为![]() ,乙能攻克的概率为
,乙能攻克的概率为![]() ,丙能攻克的概率为
,丙能攻克的概率为![]() .
.
(1)求这一技术难题被攻克的概率;
(2)现假定这一技术难题已被攻克,上级决定奖励![]() 万元.奖励规则如下:若只有一人攻克,则此人获得全部奖金
万元.奖励规则如下:若只有一人攻克,则此人获得全部奖金![]() 万元;若只有两人攻克,则奖金奖给此二人,每人各得
万元;若只有两人攻克,则奖金奖给此二人,每人各得![]() 万元;若三人均攻克,则奖金奖给此三人,每人各得
万元;若三人均攻克,则奖金奖给此三人,每人各得![]() 万元.设乙、丙两人得到的奖金数的和为X,求X的分布列和均值.
万元.设乙、丙两人得到的奖金数的和为X,求X的分布列和均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com