
分析 (Ⅰ)根据正弦定理,三角函数恒等变换的应用化简已知等式可得2sinCcosB=sinC,结合sinC≠0,可求$cosB=\frac{1}{2}$,结合范围B∈(0,π),可求B的值.
(Ⅱ)解法一:延长BD至点E,使得DE=BD,连接AE,CE.可求$∠BCE=\frac{2π}{3}$,BE=14.在△BCE中,根据余弦定理,得CE2+6CE-160=0,解得CE,AB的值,利用三角形面积公式即可计算得解.
解法二:利用向量加法可得$\overrightarrow{BD}=\frac{1}{2}(\overrightarrow{BA}+\overrightarrow{BC})$,平方可得$4{\overrightarrow{BD}^2}={\overrightarrow{BA}^2}+{\overrightarrow{BC}^2}+2\overrightarrow{BA}•\overrightarrow{BC}$,代入解得AB的值,利用三角形面积公式即可得解.
解法三:设AB=x,CD=DA=y.根据余弦定理,可得4y2=x2-6x+36…①,进而可求$cos∠BDC=\frac{{{y^2}+13}}{14y}$,$cos∠BDA=\frac{{{y^2}-{x^2}+49}}{14y}$.化简可得2y2=x2-62…②. 由①②可得AB的值,利用三角形面积公式即可得解.
解答 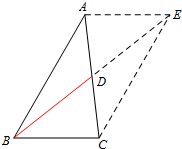 解:(Ⅰ)根据正弦定理,由(2c-a)cosB=bcosA,
解:(Ⅰ)根据正弦定理,由(2c-a)cosB=bcosA,
可得(2sinC-sinA)cosB=sinBcosA,
整理得2sinCcosB=sinAcosB+sinBcosA,
所以2sinCcosB=sinC,
因为sinC≠0,
所以$cosB=\frac{1}{2}$,
又因为B∈(0,π),
所以$B=\frac{π}{3}$.…(6分)
(Ⅱ)如图,延长BD至点E,使得DE=BD,连接AE,CE.
因为D为AC的中点,所以四边形ABCE为平行四边形,
所以$∠BCE=\frac{2π}{3}$,BE=14.
在△BCE中,根据余弦定理,得$B{E^2}=B{C^2}+C{E^2}-2BC•CE•cos\frac{2π}{3}$,
即CE2+6CE-160=0,解得CE=10,所以AB=CE=10.
所以△ABC的面积$S=\frac{1}{2}AB•BC•sinB=\frac{1}{2}×6×10×sin\frac{π}{3}=15\sqrt{3}$.…(12分)
解法二:(Ⅰ)同解法一.
(Ⅱ)因为BD是AC边上的中线,所以$\overrightarrow{BD}=\frac{1}{2}(\overrightarrow{BA}+\overrightarrow{BC})$,
所以$\overrightarrow{BD}=\frac{1}{2}(\overrightarrow{BA}+\overrightarrow{BC})$,即$4{\overrightarrow{BD}^2}={\overrightarrow{BA}^2}+{\overrightarrow{BC}^2}+2\overrightarrow{BA}•\overrightarrow{BC}$.
所以$4×{7^2}=|\overrightarrow{BA}{|^2}+{6^2}+2×6×|{\overrightarrow{BA}}|×cos\frac{π}{3}$,即${|{\overrightarrow{BA}}|^2}+6|{\overrightarrow{BA}}|-160=0$,
解得$|\overrightarrow{BA}|=10$,即AB=10.
所以△ABC的面积$S=\frac{1}{2}AB•BC•sinB=\frac{1}{2}×6×10×sin\frac{π}{3}=15\sqrt{3}$.
解法三:(Ⅰ)同解法一.
(Ⅱ)设AB=x,CD=DA=y.
在△ABC中,根据余弦定理,可得$A{C^2}=A{B^2}+B{C^2}-2AB•BC•cos\frac{π}{3}$,
即4y2=x2-6x+36…①. 在△BCD中,根据余弦定理可得,$cos∠BDC=\frac{{B{D^2}+D{C^2}-B{C^2}}}{2BD•DC}=\frac{{{7^2}+{y^2}-{6^2}}}{2×7y}=\frac{{{y^2}+13}}{14y}$.
在△ABD中,同理可得,$cos∠BDA=\frac{{B{D^2}+A{D^2}-A{B^2}}}{2BD•AD}=\frac{{{7^2}+{y^2}-{x^2}}}{2×7y}=\frac{{{y^2}-{x^2}+49}}{14y}$.
因为∠BDC+∠BDA=π,
所以cos∠BDC=-cos∠BDA,
所以y2+13=-(y2-x2+49),
即2y2=x2-62…②. 由①②可得x2+6x-160=0,
所以x=10,即AB=10.
所以△ABC的面积$S=\frac{1}{2}AB•BC•sinB=\frac{1}{2}×6×10×sin\frac{π}{3}=15\sqrt{3}$.
点评 本题主要考查了正弦定理,三角函数恒等变换的应用,余弦定理,三角形面积公式,平面向量的运算在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:选择题
| A. | $[\frac{1}{4},3]$ | B. | $[\frac{1}{2},5]$ | C. | $[\frac{13}{4},5]$ | D. | $[-\frac{27}{4},-5]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $C_{2011}^3$ | B. | $C_{2011}^4$ | C. | $C_{2012}^3$ | D. | $C_{2012}^4$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com