
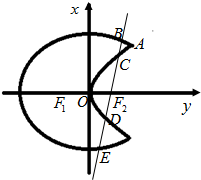
 如图,曲线C1是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的一部分,F1,F2是其两焦点.曲线C2是以原点O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的一个公共点,并且∠AF2F1为钝角.我们把由曲线C1和C2合成的曲线C称为“月食圆”.
如图,曲线C1是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的一部分,F1,F2是其两焦点.曲线C2是以原点O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的一个公共点,并且∠AF2F1为钝角.我们把由曲线C1和C2合成的曲线C称为“月食圆”.分析 (1)利用椭圆与抛物线的定义求解方程;(2)利用直线与椭圆抛物线相交问题、一元二次方程的根与系数的关系进行计算;(3)通径计算公式;(4)利用正弦定理计算.
解答 解:对于①,椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0).则2a=|AF1|+|AF2|=7+5=12,得a=6,
设A(x,y),F1(-c,0),F2(c,0),则(x+c)2+y2=72,(x-c)2+y2=52,
两式相减得xc=6,由抛物线定义可知|AF2|=x+c=5,
则c=2,x=3或x=2,c=3,又∠AF2F1为钝角,则x=2,c=3舍去.
曲线C1、C2的方程别为$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{32}$=1(-6≤x≤3)、y2=8x(0≤x≤3),故①正确;
对于②,当直线l⊥x轴时,直线l的方程为x=c,x1x2x3x4=c4
当直线l不垂直x轴时,设B(x1,y1),E(x2,y2),C(x3,y3),D(x4,y4),
联立y=$\left\{\begin{array}{l}{y=k(x-c)}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,化为(b2+a2k2)x2-2ca2k2x+a2k2c2-a2b2=0,∴x1x2=$\frac{{a}^{2}{k}^{2}{c}^{2}-{a}^{2}{b}^{2}}{{b}^{2}+{a}^{2}{k}^{2}}$,
联立 $y=\left\{\begin{array}{l}{y=k(x-c)}\\{{y}^{2}=4cx}\end{array}\right.$ 化为:k2x2-(2ck2+4c)x+k2c2=0,∴x3x4=c2.
∴x1x2x3x4≠c4.因此不为定值,故②错;
对于③,当直线l⊥x轴时,直线l的方程为x=c,从而|CD|=2p=4c,|BE|=$\frac{2{b}^{2}}{a}$,
当l与x轴垂直时,$\frac{|CD|}{|BE|}$≠$\frac{3}{4}$,故③错
对于④,连接BF1,EF2,在△BF1F2中,由正弦定理可得$\frac{2c}{sinα}=\frac{B{F}_{1}}{sinγ}=\frac{B{F}_{2}}{sinβ}=\frac{B{F}_{1}+B{F}_{2}}{sinγ+sinβ}=\frac{2a}{sinγ+sinβ}$:正确.∴e=$\frac{c}{a}\\;\\;=\frac{sinα}{sinβ+sinγ}$,故④正确.
故答案:①④
点评 本题考查了椭圆与抛物线的标准方程、直线与椭圆抛物线相交问题、一元二次方程的根与系数的关系、通经计算公式、正弦定理,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (-1,+∞) | C. | (-1,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com