
| A. | (-2,-1) | B. | (-1,+∞) | C. | (-1,2) | D. | (2,+∞) |
分析 设g(x)=f(x+1)-ln(x+2)-2-ex+1-3x,x>-2,求导g′(x)=f′(x+1)-$\frac{1}{x+2}$-ex+1-3,由f′(x)<2,f′(x+1)-3<0,由-$\frac{1}{x+2}$-ex+1<0恒成立,因此g′(x)<0恒成立,则g(x)在(-2,+∞)单调递减,根据函数的奇偶性可知f(0)=0,可得g(-1)=0,则原不等式可转化成,g(x)=g(-1),由函数的单调性即可求得-2<x<-1.
解答 解:由题意可知:设g(x)=f(x+1)-ln(x+2)-2-ex+1-3x,x>-2,
求导g′(x)=f′(x+1)-$\frac{1}{x+2}$-ex+1-3,
由f′(x)<2,即f′(x)-2<0,
f′(x+1)-3<0,
由函数的单调性可知:-$\frac{1}{x+2}$-ex+1<0恒成立,
∴g′(x)<0恒成立,
∴g(x)在(-2,+∞)单调递减,
由y=f(x)为奇函数,则f(0)=0
∴g(-1)=f(0)-ln1-2-e0+3=0,
由f(x+1)-ln(x+2)-2>ex+1+3x,即g(x)>0=g(-1),
由函数的单调递减,
∴-2<x<-1,
∴不等式f(x+1)-ln(x+2)-2>ex+1+3x的解集(-2,-1),
故选A.
点评 本题考查函数的单调性与导数的关系,考查利用导数求函数的单调性,考查不等式的解集的求法,考查转化思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | M∩N={ 4,6 } | B. | M∪N=U | C. | (∁UN )∪M=U | D. | (∁UM)∩N=N |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
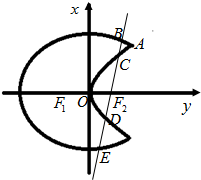 如图,曲线C1是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的一部分,F1,F2是其两焦点.曲线C2是以原点O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的一个公共点,并且∠AF2F1为钝角.我们把由曲线C1和C2合成的曲线C称为“月食圆”.
如图,曲线C1是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的一部分,F1,F2是其两焦点.曲线C2是以原点O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的一个公共点,并且∠AF2F1为钝角.我们把由曲线C1和C2合成的曲线C称为“月食圆”.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x>0,cosx+sinx>1 | B. | ?x0≤0,cosx0+sinx0≤1 | ||
| C. | ?x>0,cosx+sinx≤1 | D. | ?x0>0,cosx0+sinx0≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,∠ABC=120°,G为线段PC上的点,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,∠ABC=120°,G为线段PC上的点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
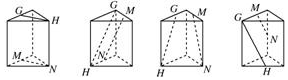
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com