
| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | 2 |
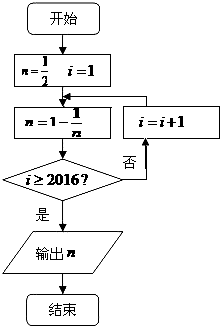
分析 模拟执行程序,依次写出每次循环得到的i,n的值,观察规律可得n的取值以3为周期,从而有当i=2016时,满足i≥2016,退出循环,输出n的值,从而得解.
解答 解:模拟程序的运行,可得
n=$\frac{1}{2}$,i=1
n=-1,
不满足条件i≥2016,执行循环体,i=2,n=2
不满足条件i≥2016,执行循环体,i=3,n=$\frac{1}{2}$
不满足条件i≥2016,执行循环体,i=4,n=-1
…
观察规律可知,n的取值周期为3,由于2016=672×3,可得:
不满足条件i≥2016,执行循环体,i=2015,n=2
不满足条件i≥2016,执行循环体,i=2016,n=$\frac{1}{2}$
满足条件i≥2016,退出循环,输出n的值为$\frac{1}{2}$.
故选:C.
点评 本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答,属于基本知识的考查.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{3}$或-$\frac{3}{5}$ | B. | -$\frac{3}{2}$或-$\frac{2}{3}$ | C. | -$\frac{5}{4}$或-$\frac{4}{5}$ | D. | -$\frac{4}{3}$或-$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
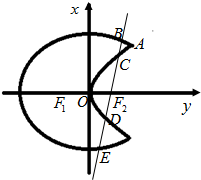 如图,曲线C1是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的一部分,F1,F2是其两焦点.曲线C2是以原点O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的一个公共点,并且∠AF2F1为钝角.我们把由曲线C1和C2合成的曲线C称为“月食圆”.
如图,曲线C1是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的一部分,F1,F2是其两焦点.曲线C2是以原点O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的一个公共点,并且∠AF2F1为钝角.我们把由曲线C1和C2合成的曲线C称为“月食圆”.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{3}{2}$] | B. | [$\frac{3}{2}$,+∞) | C. | (-1,$\frac{3}{2}$] | D. | [$\frac{3}{2}$,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,∠ABC=120°,G为线段PC上的点,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,∠ABC=120°,G为线段PC上的点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4,8,6 | B. | 6,8,4 | C. | 6,10,2 | D. | 8,4,6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com