
分析 将所证的关系式作差(ax+by)2-(ax2+by2)=a(a-1)x2+b(b-1)y2+2abxy利用a+b=1,整理,可得a(a-1)x2+b(b-1)y2+2abxy=-ab(x-y)2≤0,当且仅当x=y时等号成立.
解答 证明:(ax+by)2-(ax2+by2)=a(a-1)x2+b(b-1)y2+2abxy,
因为a+b=1,
所以a-1=-b,b-1=-a,
又a,b均为正数,
所以a(a-1)x2+b(b-1)y2+2abxy=-ab(x2+y2-2xy)=-ab(x-y)2≤0,当且仅当x=y时等号成立.
所以ax2+by2≥(ax+by)2.
点评 本题考查不等式的证明,着重考查作差法的应用,突出考查等价转化思想与逻辑推理能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
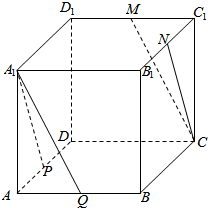 在正方体ABCD-A1B1C1D1中,P,Q,M,N分别为AD,AB,C1D1,B1C1的中点,求证:
在正方体ABCD-A1B1C1D1中,P,Q,M,N分别为AD,AB,C1D1,B1C1的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
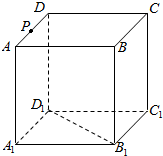 如图所示,正方体ABCD-A1B1C1D1的棱长为a,点P是棱AD上一点,且AP=$\frac{a}{3}$,过点B1,D1,P的平面交底面ABCD于PQ,Q在直线CD上,则PQ=$\frac{\sqrt{2}a}{3}$.
如图所示,正方体ABCD-A1B1C1D1的棱长为a,点P是棱AD上一点,且AP=$\frac{a}{3}$,过点B1,D1,P的平面交底面ABCD于PQ,Q在直线CD上,则PQ=$\frac{\sqrt{2}a}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
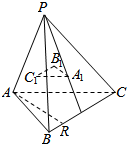 如图,P是△ABC所在平面外的一点,A1,B1,C1依次是△PBC,△PAC,△PAB的重心,AR是平面ABC内的任意一条直线,求证:AR∥平面A1B1C1.
如图,P是△ABC所在平面外的一点,A1,B1,C1依次是△PBC,△PAC,△PAB的重心,AR是平面ABC内的任意一条直线,求证:AR∥平面A1B1C1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{π}}{3}$ | B. | $\frac{\sqrt{π}}{2}$ | C. | $\frac{\sqrt{3π}}{3}$ | D. | $\frac{\sqrt{3π}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinα>0,cosα>0 | B. | sinα<0,cosα<0 | C. | sinα>0,cosα<0 | D. | sinα<0,cosα>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com