
分析 将Q的坐标化为直角坐标,由两点的距离公式,结合三角函数的同角公式和配方法,以及正弦函数的值域,即可得到最大值.
解答 解:设P(cosθ,2sinθ),
Q($\sqrt{3}$,$\frac{π}{2}$)化为直角坐标为Q(0,$\sqrt{3}$),
即有|PQ|=$\sqrt{(cosθ-0)^{2}+(2sinθ-\sqrt{3})^{2}}$
=$\sqrt{co{s}^{2}θ+4si{n}^{2}θ-4\sqrt{3}sinθ+3}$
=$\sqrt{3si{n}^{2}θ-4\sqrt{3}sinθ+4}$=|$\sqrt{3}$sinθ-2|,
由-1≤sinθ≤1,
即有sinθ=-1,|PQ|取得最大值2+$\sqrt{3}$.
故答案为:2+$\sqrt{3}$.
点评 本题考查极坐标和直角坐标的互化,考查椭圆的参数方程的运用,同时考查三角函数的化简和求值,运用正弦函数的值域是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
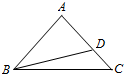 如图,在△ABC中,AB=AC,D在线段AC上,且AC=$\sqrt{2}$AD,BD=1.
如图,在△ABC中,AB=AC,D在线段AC上,且AC=$\sqrt{2}$AD,BD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin1<2sin$\frac{1}{2}<3sin\frac{1}{3}$ | B. | 3sin$\frac{1}{3}<2sin\frac{1}{2}$<sin1 | ||
| C. | sin1<3sin$\frac{1}{3}<2sin\frac{1}{2}$ | D. | 2sin$\frac{1}{2}<sin1<3sin\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (1)求⊙P的半径(用θ表示);
(1)求⊙P的半径(用θ表示);查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com