
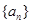 的前
的前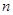 项和
项和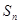 满足
满足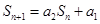 ,其中
,其中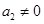
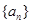 首项为1的等比数列;
首项为1的等比数列;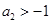 ,求证:
,求证: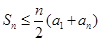 ,并给指出等号成立的充要条件。
,并给指出等号成立的充要条件。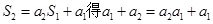 ,即
,即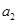
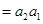 ,
,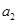
 ,故
,故 ,得
,得
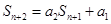 ,
,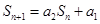
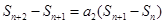 ,即
,即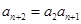 由
由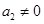 ,知
,知 ,
,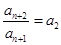 综上
综上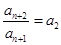 对所有
对所有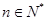 成立,从而
成立,从而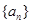 是首项为1,公比为
是首项为1,公比为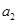 的等比数列。
的等比数列。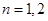 时,显然
时,显然 ,等号成立
,等号成立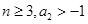 且
且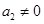 ,由(Ⅰ)知
,由(Ⅰ)知 ,
,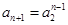 所以要证的不等式化为
所以要证的不等式化为 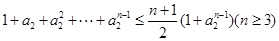
 ,当
,当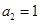 时,上面不等式的等号成立
时,上面不等式的等号成立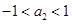 时,
时,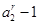 与
与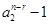
 同为负;当
同为负;当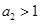 时
时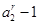
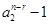
 同为正,因此当
同为正,因此当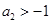 且
且 时,
时,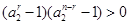 ,即
,即

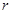 从1到
从1到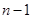 求各得
求各得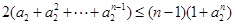

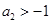 且
且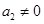 时,有
时,有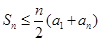 ,当且仅当
,当且仅当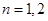 或
或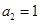 时等号成立。
时等号成立。

科目:高中数学 来源:不详 题型:解答题
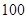 万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.设经过
万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.设经过 年后该项目的资金为
年后该项目的资金为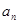 万元.
万元.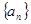 的前三项
的前三项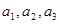 ,并猜想写出通项
,并猜想写出通项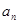 .
. 千万元.
千万元.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 }满足
}满足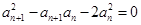 (
(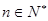 ),且
),且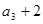 是
是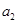 ,
,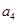 的等差中项.
的等差中项.  }的通项公式
}的通项公式 ;
;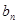 =
=
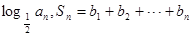 ,是否存在正整数
,是否存在正整数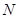 ,使
,使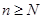 时,不等式
时,不等式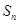
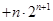
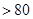 恒成立,若存在,求
恒成立,若存在,求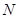 的值;不存在,说明理由.
的值;不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
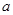 、
、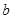 、
、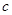 成等差数列,则
成等差数列,则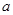 、
、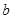 、
、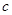 之比为
之比为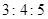 ;
;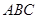 的三内角
的三内角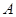 、
、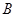 、
、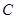 成等差数列,则
成等差数列,则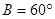 ;
;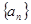 的前
的前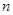 项和为
项和为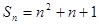 ,则
,则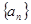 的通项公式
的通项公式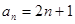 ;
;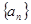 的前
的前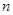 项和为
项和为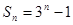 ,则
,则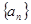 为等比数列。
为等比数列。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com