
已知数列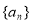 的前
的前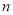 项和为
项和为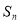 ,且
,且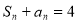 ,
,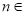 N*
N*
(1)求数列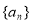 的通项公式;
的通项公式;
(2)已知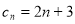 (
(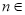 N*),记
N*),记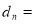
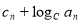 (
(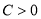 且
且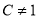 ),是否存在这样的常数
),是否存在这样的常数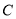 ,使得数列
,使得数列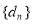 是常数列,若存在,求出
是常数列,若存在,求出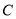 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)若数列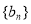 ,对于任意的正整数
,对于任意的正整数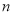 ,均有
,均有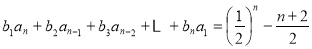 成立,求证:数列
成立,求证:数列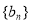 是等差数列;
是等差数列;
(1) 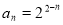 (
(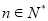 );(2)
);(2) 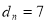 ;(3)
;(3)
【解析】
试题分析:(1)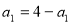 ,所以
,所以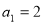 ,由
,由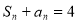 得
得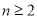 时,
时,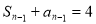 ,两式相减得,
,两式相减得,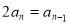 ,
,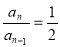 , 数列
, 数列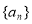 是以2为首项,公比为
是以2为首项,公比为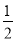 的等比数列,即可求出通项公式;(2)由于数列
的等比数列,即可求出通项公式;(2)由于数列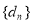 是常数列,可得
是常数列,可得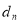 =
=
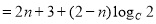
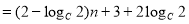 为常数,故只有
为常数,故只有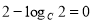 ,解得
,解得 ,可得
,可得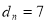 ;(3)
;(3)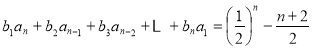 ①
①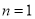 ,
,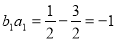 ,其中
,其中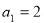 ,所以
,所以 ;当
;当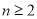 时,
时,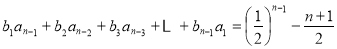 ②;②式两边同时乘以
②;②式两边同时乘以 得,
得, ③;①式减去③得,
③;①式减去③得,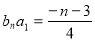 ,所以
,所以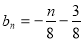 且
且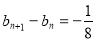 可得数列
可得数列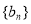 是以
是以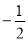 为首项,公差为
为首项,公差为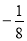 的等差数列.
的等差数列.
试题解析:【解析】
(1)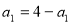 ,所以
,所以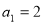 1分
1分
由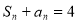 得
得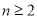 时,
时,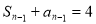 2分
2分
两式相减得,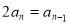 ,
,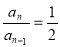 ,3分
,3分
数列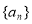 是以2为首项,公比为
是以2为首项,公比为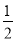 的等比数列,所以
的等比数列,所以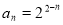 (
(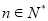 )5分
)5分
(2)由于数列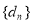 是常数列
是常数列
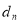 =
=
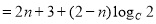 6分
6分
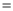
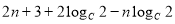
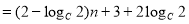 为常数7分
为常数7分
只有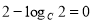 ,8分;解得
,8分;解得 ,9分
,9分
此时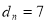 10分
10分
(3)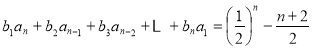 ①
①
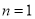 ,
,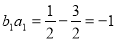 ,其中
,其中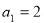 ,所以
,所以 11分
11分
当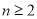 时,
时,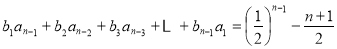 ②12分
②12分
②式两边同时乘以 得,
得, ③13分
③13分
①式减去③得,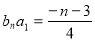 ,所以
,所以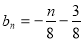 14分
14分
且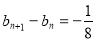 15分
15分
所以数列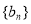 是以
是以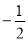 为首项,公差为
为首项,公差为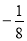 的等差数列。16分.
的等差数列。16分.
考点:1.等差数列、等比数列、常数数列的性质;2.数列的求和公式.


科目:高中数学 来源:2014-2015学年广东省惠州市高三第三次调研理科数学试卷(解析版) 题型:选择题
数列 ,满足对任意的
,满足对任意的 ,均有
,均有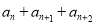 为定值.若
为定值.若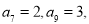
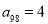 ,则数列
,则数列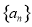 的前100项的和
的前100项的和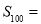 ( ).
( ).
A.132 B.299 C.68 D.99
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市西城区高三上学期期末考试理科数学试卷(解析版) 题型:选择题
一个四棱锥的三视图如图所示,那么对于这个四棱锥,下列说法中正确的是( )
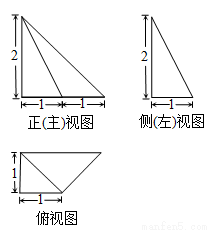
(A)最长棱的棱长为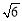
(B)最长棱的棱长为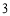
(C)侧面四个三角形中有且仅有一个是正三角形
(D)侧面四个三角形都是直角三角形
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市普陀区高三上学期质量调研文科数学试卷(解析版) 题型:选择题
要得到函数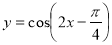 的图像,只需将函数
的图像,只需将函数 的图像( )
的图像( )
A. 向左平移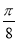 个单位 B.向右平移
个单位 B.向右平移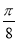 个单位
个单位
C.向左平移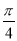 个单位 D.向右平移
个单位 D.向右平移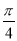 个单位
个单位
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市普陀区高三上学期质量调研理科数学试卷(解析版) 题型:选择题
“点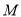 在曲线
在曲线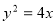 上”是“点
上”是“点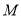 的坐标满足方程
的坐标满足方程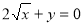 ”的( )
”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分也非必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com