练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．小晶用圆、三角形、正方形按一定规律画图，前八个图形如图所示，则猜测第2017个图形中共含有的正方形个数为336．

    分析 通过观察，分析、归纳并发现其中的规律，并应用发现的规律解决问题．

    解答 解：通过观察发现一个三角形等于两个圆，一个正方形等于三个三角形，即一个正方形等于六个圆．
    又2017=336×6+1，故应有336个正方形．
    故答案为336．

    点评 本题考查了图形的变化类问题，解题的关键是仔细的观察图形并从中发现规律，然后利用发现的规律解题即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    13．若x 满足${x^{\frac{1}{2}}}-{x^{-\frac{1}{2}}}=2\sqrt{3}$，则x+x-1=14．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．设函数f（x）=sin2（x+$\frac{π}{4}$）-cos2（x+$\frac{π}{4}$）（x∈R），则函数f（x）是（　　）
    A．最小正周期为π的奇函数B．最小正周期为π的偶函数
    C．最小正周期为$\frac{π}{2}$的奇函数D．最小正周期为$\frac{π}{2}$的偶函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．以模型y=cekx去拟合一组数据时，为了求出回归方程，设z=lny，将其变换后得到线性方程z=0.3x+4，则c，k的值分别是e4和0.3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知曲线C的极坐标方程是ρ-2cosθ-4sinθ=0，以极点为在平面直角坐标系的原点，极轴为x轴的正半轴建立平面直角坐标系xoy，直线的参数方程为$\left\{\begin{array}{l}x=\frac{{\sqrt{3}}}{2}t\\ y=1+\frac{1}{2}t\end{array}\right.$（t为参数）．
    （1）将曲线C的极坐标方程化为直角坐标方程，将直线l的参数方程化为普通方程；
    （2）若直线l与曲线C相交于A，B两点，与y轴交于点M，求（|MA|+|MB|）2的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．若点A（a，b）（ a≠b）在矩阵M=$|\begin{array}{l}{cosx}&{-sinx}\\{sinx}&{cosx}\end{array}|$对应变换的作用下得到的点为B（-b，a），
    （1）求矩阵M的逆矩阵；
    （2）求曲线C：x2+y2=1在矩阵N=$|\begin{array}{l}{0}&{\frac{1}{2}}\\{1}&{0}\end{array}|$所对应变换的作用下得到的新的曲线C′的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知函数$f（x）=\left\{\begin{array}{l}3x-\frac{1}{2}，x＜1\\{2^x}，x≥1\end{array}\right.$，则$f[f（\frac{1}{2}）]$=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．执行如图所示的程序框图，则输出m的值为（　　）
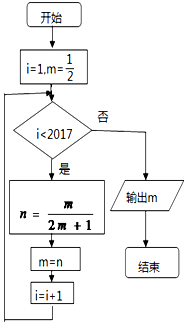
    A．$\frac{1}{2016}$B．$\frac{1}{2017}$C．$\frac{1}{4032}$D．$\frac{1}{4034}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑，如图，网格纸上正方形小格的边长为1，图中粗线画出的是某几何体毛坯的三视图，第一次切削，将该毛坯得到一个表面积最大的长方体，第二次切削沿长方体的对角面刨开，得到两个三棱柱，第三次切削将两个三棱柱分别沿棱和表面的对角线刨开得到两个鳖臑和两个阳马，则阳马与鳖臑的体积之比为（　　）
    A．3：1B．2：1C．1：1D．1：2

    查看答案和解析>>

    同步练习册答案