
分析 (1)设A(x1,y1),B(x2,y2),由${y}_{1}^{2}=6{x}_{1}$,${y}_{2}^{2}$=6x2,可得$\frac{({y}_{1}-{y}_{2})({y}_{1}+{y}_{2})}{{x}_{1}-{x}_{2}}$=6,利用斜率与中点坐标公式即可得出;
(2)直线l的方程为y-1=x-4,化为y=x-3;与抛物线方程联立化为x2-12x+9=0,利用根与系数的关系、弦长公式可得|AB|,再利用点到直线的距离公式可得原点O到直线l的距离,可得S△AOB=$\frac{1}{2}|AB|•d$.
解答 解:(1)设A(x1,y1),B(x2,y2),则$\frac{{x}_{1}+{x}_{2}}{2}$=4,$\frac{{y}_{1}+{y}_{2}}{2}$=1,$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=kAB,
∵${y}_{1}^{2}=6{x}_{1}$,${y}_{2}^{2}$=6x2,∴$\frac{({y}_{1}-{y}_{2})({y}_{1}+{y}_{2})}{{x}_{1}-{x}_{2}}$=6,∴2kAB=6,解得kAB=3.
∴直线l的方程为:y-1=3(x-4),化为3x-y-11=0.
(2)直线l的方程为y-1=x-4,化为y=x-3;
联立$\left\{\begin{array}{l}{y=x-3}\\{{y}^{2}=6x}\end{array}\right.$,化为x2-12x+9=0,
∴x1+x2=12,x1x2=9,
∴|AB|=$\sqrt{2[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{2(1{2}^{2}-4×9)}$=$6\sqrt{6}$.
原点O到直线l的距离d=$\frac{|0-3|}{\sqrt{2}}$=$\frac{3}{\sqrt{2}}$,
∴S△AOB=$\frac{1}{2}|AB|•d$=$\frac{1}{2}×6\sqrt{6}×\frac{3}{\sqrt{2}}$=$9\sqrt{3}$.
点评 本题考查了抛物线的标准方程及其性质、斜率与中点坐标公式、直线与与抛物线相交问题转化为方程联立得到根与系数的关系、弦长公式、点到直线的距离公式、三角形的面积计算公式,考查了推理能力与技能数列,属于中档题.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
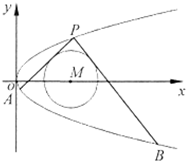 已知曲线C:y2=2px(p>0)过定点(1,1),点P是曲线C上的动点,过点P的圆M:(x-t)2+y2=1(t>1)的切线l1,l2分别交曲线C于另外两点A,B.
已知曲线C:y2=2px(p>0)过定点(1,1),点P是曲线C上的动点,过点P的圆M:(x-t)2+y2=1(t>1)的切线l1,l2分别交曲线C于另外两点A,B.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{2}$ | B. | 8 | C. | 8$\sqrt{2}$ | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于原点对称 | B. | 关于y轴对称 | ||
| C. | 关于点($\frac{π}{4}$,0)对称 | D. | 关于直线x=$\frac{π}{4}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com